a: HA=căn 20^2-12^2=16cm

AC=5/3*16=80/3(cm)

Xét ΔHAC vuông tại H và ΔHBA vuông tại H có

AC/BA=HA/HB(=4/3)

=>ΔHAC đồng dạng với ΔHBA

b: HC=căn AC^2-AH^2=64/3(cm)

=>BC=12+64/3=100/3(cm)

Xét ΔBHA và ΔBAC có

BH/BA=BA/BC

góc B chung

=>ΔBHA đồng dạng với ΔBAC

=>góc BAC=góc BHA=90 độ

=>ĐPCM

a: Xét ΔABH vuông tại H và ΔKIH vuông tại H có

HA=HK

HB=HI

=>ΔABH=ΔKIH

b: ΔABH=ΔKIH

=>góc ABH=góc KIH

=>AB//IK

c: IK//AB

AB vuông góc AC

=>IK vuông góc AC

=>I,K,E thẳng hàng

d: Xét tứ giác ABKI có

H là trung điểm chung của AK và BI

AK vuông góc BI

=>ABKI là hình thoi

=>AB=AI=IK

=>IK=ID

=>góc IKD=góc IDK

chịu

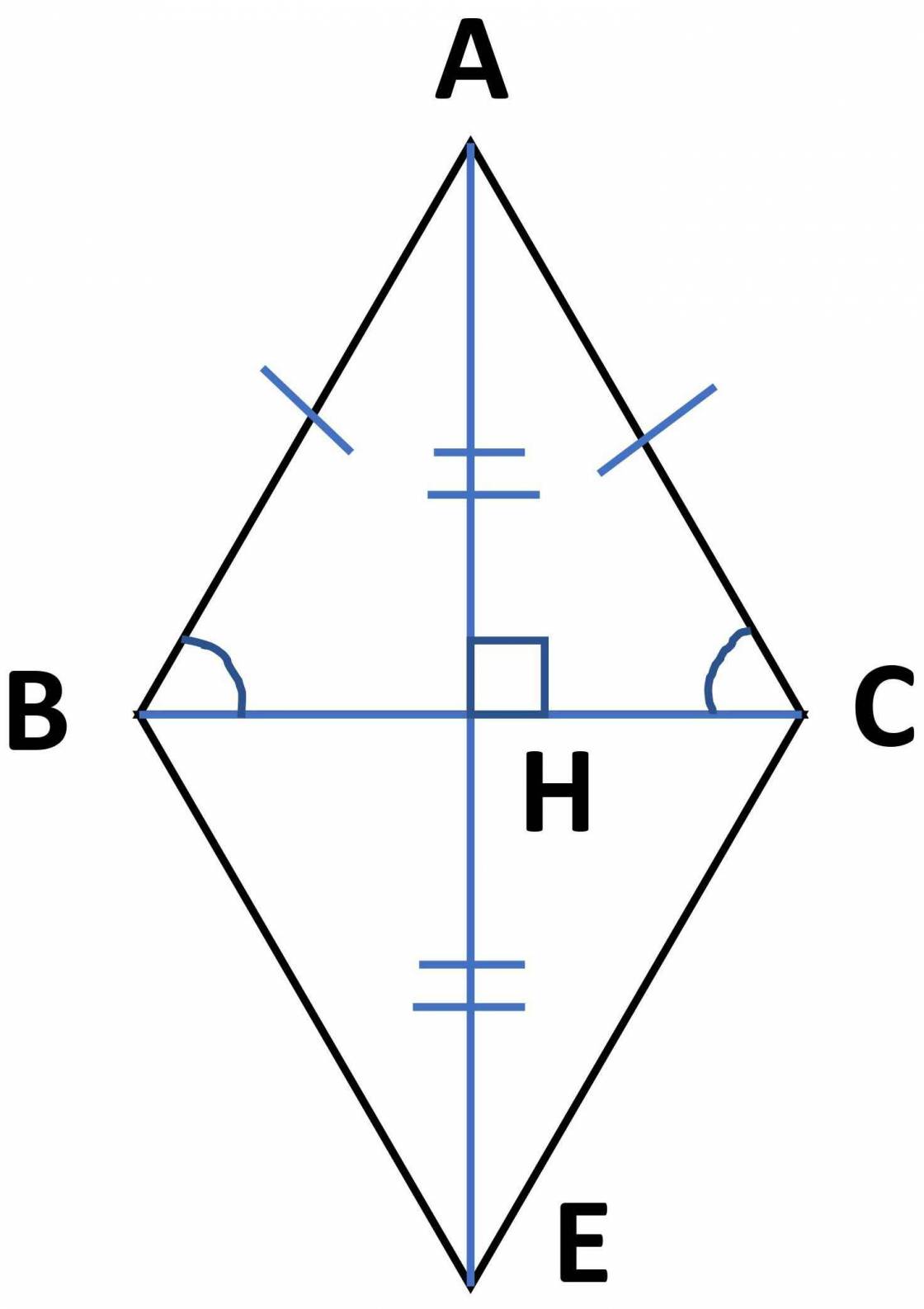
a) xét ΔABH và ΔACH, ta có :

AB = AC (giả thiết)

\(\widehat{ABC}=\widehat{ACB}\)  (vì AB = AC => đó là tam giác cân, mà tam giác cân thì có 2 góc ở đáy bằng nhau)

AH là cạnh chung

ð ΔABH = ΔACH (c.c.c)

b) vì ΔABH = ΔACH, nên :

=> HB = HC (2 cạnh tương ứng)

c) hơi khó nha !

ai trl trc thì mk cho hen!!!

a, Xét hai tam giác ABH và tam giác ADH có

BH=HD(giả thiết)

góc BHA=góc DHA(=90 độ)

AH chung

Suy ra ABH=ADH(dpcm)

b,c,d dài qúa mik ko ghi nổi bạn thông cảm nhé^^

Bài làm

a) Xét tam giác ABH vuông tại H có:

Theo định lí Pytago có:

AB² = AH² + HB² 

hay AB² = 6² + 4² 

=> AB² = 36 + 16

=> AB² = 52

=> AB = \(2\sqrt{13}\) \(\approx\)7,2 ( cm )

b) Xét tam giác AHC vuông ở H có:

Theo định lí Pytago có: 

AC² = AH² + HC² 

Hay AC² = 6² + 9² 

=> AC² = 36 + 81

=> AC² = 117

=> AC = \(3\sqrt{13}\)\(\approx\)10,8 ( cm )

Ta có: BC = 9 + 4 = 13

=> BC² = 13² = 169 

AB² + AC² = \(\left(2\sqrt{13}\right)^2+\left(3\sqrt{13}\right)^2=52+117=169\)

=> BC² = AB² + AC² 

=> Tam giác ABC vuông tại A ( Theo định lí Pytago đảo )

c) Vì DE song song với AH

Theo định lí Thalets có:

\(\frac{CH}{HD}=\frac{AC}{AE}\)

hay \(\frac{9}{6}=\frac{3\sqrt{13}}{AE}\)

=> AE = \(\frac{6.3\sqrt{13}}{9}=\frac{18\sqrt{13}}{9}=2\sqrt{13}\)

Mà AB = \(2\sqrt{13}\)

=> AE = AB ( = \(2\sqrt{13}\)) ( đpcm )

\(\dfrac{1}{2}\) AB.AB là sao ạ??

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

=>ΔAHB=ΔAHC

b: Xét tứ giác AHED có

B là trung điểm chung của AE và HD

=>AHED là hình bình hành

=>DE//AH