a) Phương trình đường tròn \(\left( C \right)\) là: \({\left( {x + 2} \right)^2} + {\left( {y - 5} \right)^2} = 49\).

b) Bán kính đường tròn là: \(R = IA = \sqrt {{{\left( { - 2 - 1} \right)}^2} + {{\left( {2 - \left( { - 2} \right)} \right)}^2}}  = 5\)

Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 25\)

c) Gọi \(I\left( {a;b} \right)\) là trung điểm AB. Vậy tọa độ điểm I là: \(I\left( { - 2;1} \right)\)

Bán kính đường tròn là: \[R = IA = \sqrt {{{\left( { - 1 + 2} \right)}^2} + {{\left( { - 3 - 1} \right)}^2}}  = \sqrt {17} \]

Phương trình đường tròn là: \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} = 17\)

d) Bán kính đường tròn là: \(R = \frac{{\left| {1 + 2.3 + 3} \right|}}{{\sqrt {{1^2} + {2^2}} }} = 2\sqrt 5 \)

Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 20\)

a) (C) có tâm I và đi qua M nên bán kính R = IM

Ta có: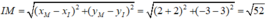 

Vậy đường tròn (C) : (x + 2)2 + (y – 3)2 = 52.

b) (C) tiếp xúc với (Δ) : x – 2y + 7 = 0

⇒ d(I; Δ) = R

Mà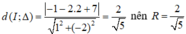 

Vậy đường tròn (C) :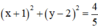 

c) (C) có đường kính AB nên (C) có :

+ tâm I là trung điểm của AB

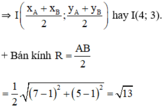
Vậy đường tròn (C) : (x – 4)2 + (y – 3)2 = 13.

a) Đường tròn (C) tâm \(I(1;5)\), bán kính \(r = 4\) có phương trình là: \({\left( {x - 1} \right)^2} + {\left( {y - 5} \right)^2} = 16\)

b) \(MN = \sqrt {{{\left( {9 - 3} \right)}^2} + {{\left( {3 - ( - 1)} \right)}^2}}  = 2\sqrt {13} \), suy ra bán kính là \(\sqrt {13} \)

Tâm của đường tròn là trung điểm của MN: \(I(6;1)\)

Đường tròn (C) tâm \(I\left( {6;1} \right)\)và bán kính là \(\sqrt {13} \) có phương trình: \({\left( {x - 6} \right)^2} + {\left( {y - 1} \right)^2} = 13\)

c) Ta có bán kính của đường tròn \(r = d\left( {I,d} \right) = \frac{{\left| {5.2 - 12.1 + 11} \right|}}{{\sqrt {{5^2} + {{12}^2}} }} = \frac{9}{{13}}\)

Đường tròn (C) tâm \(I\left( {2;1} \right)\)và bán kính là \(\frac{9}{{13}}\) có phương trình: \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{81}}{{169}}\)

d) Bán kính của đường tròn là \(r = AB = \sqrt {{{\left( {4 - 1} \right)}^2} + {{\left( {( - 5) - ( - 2)} \right)}^2}}  = 3\sqrt 2 \)

Đường tròn (C) tâm \(A(1; - 2)\)và bán kính là \(3\sqrt 2 \) có phương trình: \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 18\)

a) Viết phương trình tổng quát của AB và tính diện tích tam giác ABC

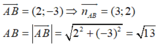
Phương trình tổng quát của AB là: 3(x - 1) + 2(y - 2) = 0 ⇔ 3x + 2y - 7 = 0

Kẻ CH ⊥ AB, (H ∈ AB)

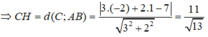
Diện tích tam giác ABC là:

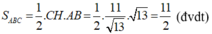
b) Viết phương trình đường tròn đường kính AB

Gọi I là trung điểm của AB

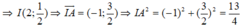
Đường tròn đường kính AB là đường tròn tâm I bán kính IA:

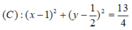
\(\overrightarrow{BA}=\left(2;4\right)\Rightarrow AB=\sqrt{2^2+4^2}=2\sqrt{5}\)

Gọi M là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}M\left(-1;0\right)\\AM=\dfrac{AB}{2}=\sqrt{5}\end{matrix}\right.\)

Đường tròn đường kính AB có tâm M và bán kính \(R=AM\) nên có pt:

\(\left(x+1\right)^2+y^2=5\)

\(\overrightarrow{AB}=\left(6;-2\right)\Rightarrow AB=2\sqrt{10}\)

Gọi I là trung điểm AB \(\Rightarrow I\left(1;4\right)\)

ĐƯờng tròn (C) nhận I là tâm và có bán kính \(R=\dfrac{AB}{2}=\sqrt{10}\)

Phương trình: \(\left(x-1\right)^2+\left(y-4\right)^2=10\)

a) Đường tròn (C) tâm \(O\left( {0;0} \right)\), bán kính \(R = 4\) có phương trình là: \({x^2} + {y^2} = 16\)

b) Đường tròn (C) tâm \(I\left( {2; - 2} \right)\), bán kính \(R = 8\) _{có phương trình:} \({\left( {x - 2} \right)^2} + {\left( {y + 2} \right)^2} = 64\)

c) Gọi M, N lần lượt là trung điểm của AB, AC ta có: \(M\left( {\frac{1}{2};\frac{5}{2}} \right),N\left( {\frac{5}{2};\frac{7}{2}} \right)\)

Đường trung trực \(\Delta \)của đoạn  thẳng AB là đường thẳng đi qua  M và nhận vt \(\overrightarrow {BA}  = (1;3)\) làm vt pháp tuyến, nên có phương trình  \(x + 3y - 8 = 0\)

Đường trung trực d của đoạn thẳng AC  là đường thẳng đi qua  N và nhận vt \(\overrightarrow {AC}  = (3; - 1)\) làm vt pháp tuyến, nên có phương trình  \(3x - y - 4 = 0\)

\(\Delta \) cắt d tại điểm \(I(2;2)\) cách đều ba điểm A, B, C suy ra đường tròn (C) cần tìm có tâm \(I(2;2)\) và có bán kính \(R = IA = \sqrt 5 \). Vậy (C) có phương trình: \({\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 5\)

a) Phương trình đường tròn là: \({\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} = 81\)

b) Bán kính đường tròn là: \(R = IM = \sqrt {{{\left( {4 - 5} \right)}^2} + {{\left( { - 1 + 2} \right)}^2}}  = \sqrt 2 \)

Phương trình đường tròn là: \({\left( {x - 5} \right)^2} + {\left( {y + 2} \right)^2} = 2\)

c) Bán kính đường tròn là: \(R = \frac{{\left| {5.1 - 12.\left( { - 1} \right) - 1} \right|}}{{\sqrt {{5^2} + {{\left( { - 12} \right)}^2}} }} = \frac{{16}}{{13}}\)

Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} = {\left( {\frac{{16}}{{13}}} \right)^2}\)

d) Gọi \(I\left( {a;b} \right)\) là trung điểm AB. Vậy tọa độ điểm I là: \(I\left( {1;1} \right)\)

Bán kính đường tròn là: \(R = IA = \sqrt {{{\left( {3 - 1} \right)}^2} + {{\left( { - 4 - 1} \right)}^2}}  = \sqrt {29} \)

Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 29\)

e) Giả sử  tâm đường tròn là điểm \(I\left( {a;b} \right)\). Ta có: \(IA = IB = IC \Leftrightarrow I{A^2} = I{B^2} = I{C^2}\)

Vì \(I{A^2} = I{B^2},I{B^2} = I{C^2}\) nên: \(\left\{ \begin{array}{l}{\left( {1 - a} \right)^2} + {\left( {1 - b} \right)^2} = {\left( {3 - a} \right)^2} + {\left( {1 - b} \right)^2}\\{\left( {3 - a} \right)^2} + {\left( {1 - b} \right)^2} = {\left( {0 - a} \right)^2} + {\left( {4 - b} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 3\end{array} \right.\)  b

Vậy \(I\left( {2;3} \right)\) và \(R = IA = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}}  = \sqrt 5 \)

Vậy phương trình đường tròn đi qua 3 điểm A,B, C là: \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 5\)