GIẢI GIÚP HA MIK NHA MỌI NGƯỜI
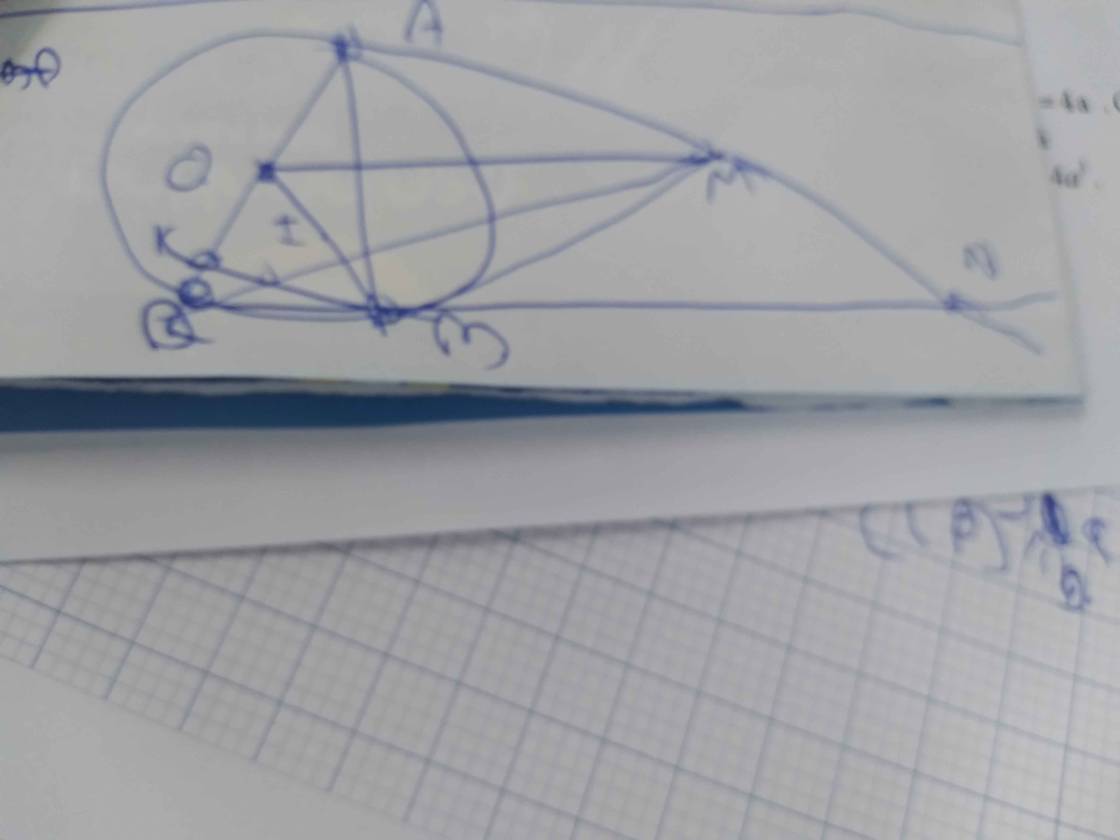
2) CHO ĐƯỜNG TRÒN (O) VÀ ĐIỂM M NẰM NGOÀI ĐƯỜNG TRÒN. VẼ 2 TIẾP TUYẾN MA,MB VỚI(O),(A,B LÀ TIẾP ĐIỂM).VẼ ĐƯỜNG KÍNH BC CỦA (O) VÀ GỌI H LÀ HÌNH CHIẾU CỦA A TRÊN ĐƯỜNG KÍNH BC CỦA(O).CHỨNG MINH MC ĐI QUA TRUG ĐIỂM I CỦA AH.
3) CHO NỬA ĐƯỜNG TRÒN (O) ĐƯỜNG KÍNH AB=2R VÀ LẤY ĐIỂM H TRÊN CẠNH OB QU H VẼ DÂY CD VUÔNG GÓC VỚI AB. TIẾP TUYẾN C CẮT CÁC TIẾP TUYẾN TẠI A,B CỦA(O) TẠI M,N; BM CẮT` CD TẠI I. CHỨNG MINH A,N,I THẲNG HÀNG.