Cho tam giác A’B’C’ có A’E’ là đường phân giác và tam giác ABC có AE là đường phân giác.Biết tam giác A’B’C’ ~ tam giác ABC theo tỉ số đồng dạng k. CM A’E’/ AE=k
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b) Ta có: ΔABC\(\sim\)ΔA'B'C'(gt)
nên \(\dfrac{S_{ABC}}{S_{A'B'C'}}=\left(\dfrac{AB}{A'B'}\right)^2\)(Định lí tỉ số diện tích của hai tam giác đồng dạng)
hay \(\dfrac{S_{ABC}}{S_{A'B'C'}}=k^2\)

Vì tam giác ABC đồng dạng với tam giác A’B’C’ theo tỉ số k nên A B A ' B ' = A C A ' C ' = B C B ' C ' = k
Suy ra A ' B ' A B = A ' C ' A C = B ' C ' B C = 1 k
Áp dụng tính chất dãy tỉ số bằng nhau ta có
A ' B ' A B = A ' C ' A C = B ' C ' B C = A ' B ' + A ' C ' + B ' C ' A B + A C + B C = 1 k
Vậy tỉ số chu vi của tam giác A’B’C’ và ABC là 1 k
Đáp án: B

a: Ta có: ΔA'B'C'∼ΔABC
nên A'B'/AB=B'C'/BC=A'C'/AC
=>A'B'/6=B'C'/12=A'C'/8=3/2
=>A'B'=9cm; B'C'=18cm; A'C'=12cm
b: Ta có: ΔA'B'C'∼ΔABC
nên \(\dfrac{C_{A'B'C'}}{C_{ABC}}=\dfrac{3}{2}\)

Vì tam giác ABC đồng dạng với tam giác A’B’C’ theo tỉ số k nên A B A ' B ' = A C A ' C ' = B C B ' C ' = k
Ta có:
A B A ' B ' = A C A ' C ' = B C B ' C ' = A B + A C + B C A ' B ' + A ' C ' + B ' C ' = P A B C P A ' B ' C ' = k
Vậy tỉ số chu vi của hai tam giác là k.
Đáp án: C

a: Xét ΔABC vuông tại A và ΔEAC vuông tại E có
góc C chung
=>ΔABC đồng dạng với ΔEAC
BC=căn 30^2+40^2=50cm
AE=30*40/50=24cm
c: góc ADF=90 độ-góc ABD
góc AFD=góc BFE=90 độ-góc DBC
mà góc ABD=góc DBC
nên góc ADF=góc AFD
=>AD=AF
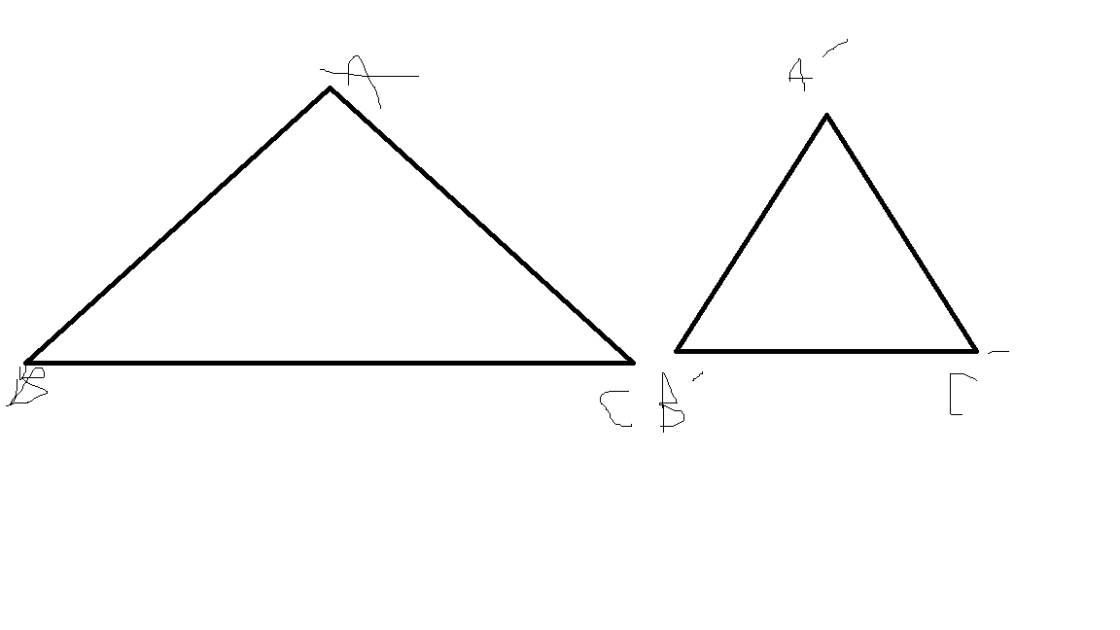
ΔA'B'C' đồng dạng với ΔABC
=>A'B'/AB=B'C'/BC=A'C'/AC=k và góc A'=góc A; góc B=góc B'; góc C'=góc C
=>góc BAE=góc B'A'E'
Xét ΔABE và ΔA'B'E' có
góc B=góc B'
góc BAE=góc B'A'E'
=>ΔABE đồng dạng với ΔA'B'E'
=>AE/A'E'=AB/A'B'
=>A'E'/AE=A'B'/AB=k