1A

2D

A D

Bài 5. Cho bốn điển A, B, C, D không nằm trên đường thẳng a, trong đó A và B thuộc cùng một nửa mặt phẳng bờ a, còn C và D thuộc nửa mặt phẳng kia. Hỏi đường thẳng a cắt đoạn thẳng nào, không cắt đoạn thẳng nào trong các đoạn thẳng nối hai trong bốn điểm A, B, C, D?

a: Ta có: ΔPQR cân tại P

mà PM là đường trung tuyến

nên PM là đường phân giác

b: Ta có: ΔPQR cân tại P

mà PM là đường trung tuyến

nên PM là đường cao

a: EK^2=EF^2+FK^2

=>ΔEFK vuông tại F

b: PQ^2<>QR^2+PR^2

=>ΔPRQ ko vuông

c: EF^2=DE^2+DF^2

=>ΔDEF vuông tại D

Sửa đề: MK\(\perp\)PQ; MN\(\perp\)PR

a: ta có: ΔPQR vuông tại P

=>\(QR^2=PQ^2+PR^2\)

=>\(QR^2=8^2+6^2=100\)

=>\(QR=\sqrt{100}=10\left(cm\right)\)

Ta có: ΔRPQ vuông tại P

mà PM là đường trung tuyến

nên \(PM=\dfrac{RQ}{2}=5\left(cm\right)\)

b: Xét tứ giác PNMK có

\(\widehat{PNM}=\widehat{PKM}=\widehat{NPK}=90^0\)

=>PNMK là hình chữ nhật

c: Xét ΔRPQ có

M là trung điểm của RQ

MK//RP

Do đó: K là trung điểm của PQ

=>PK=KQ(1)

Ta có: PKMN là hình chữ nhật

=>PK=MN(2)

Từ (1) và (2) suy ra KQ=MN

Ta có: PK//MN
K\(\in\)PQ

Do đó: NM//KQ

Xét tứ giác KQMN có

KQ//MN

KQ=MN

Do đó: KQMN là hình bình hành

=>QN cắt MK tại trung điểm của mỗi đường

mà O là trung điểm của MK

nên O là trung điểm của QN

=>OQ=ON

Xét tứ giác PMQH có

K là trung điểm chung của PQ và MN

=>PMQH là hình bình hành

Hình bình hành PMQH có PQ\(\perp\)MH

nên PMQH là hình thoi

* Vẽ hình:

- Vẽ tam giác PQR có PQ = PR = 5cm, QR = 6cm.

+ Vẽ đoạn thẳng QR = 6cm.

+ Vẽ cung tròn tâm Q và cung tròn tâm R bán kính 5cm. Hai cung tròn này cắt nhau tại P.

+ Nối PQ và PR ta được tam giác cần vẽ.

- Vẽ điểm M : Vẽ cung tròn tâm P bán kính 4,5cm cắt QR (nếu có) tại M.

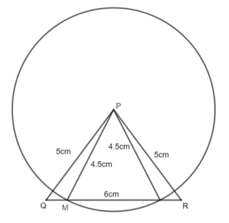
Vậy ta có thể vẽ được 2 điểm M trên đường thẳng QR để PM = 4.5cm

* Kẻ đường cao PH của ΔPQR

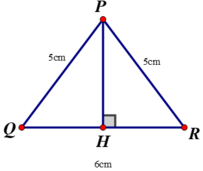
Xét hai tam giác vuông tại H: ΔPHQ và ΔPHR có

PH chung

PQ = PR ( = 5cm)

⇒ ΔPHQ = ΔPHR (cạnh huyền – cạnh góc vuông)

⇒ HQ = HR (Hai cạnh tương ứng)

Mà HQ + HR = QR = 6 cm

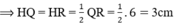
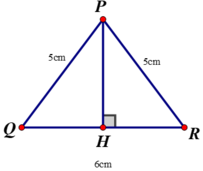
+ ΔPHR vuông tại H có PR2= PH2+ HR2(định lí Py – ta – go)

⇒ PH2= PR2– HR2= 52– 32= 16 ⇒ PH = 4cm .

Đường vuông góc PH = 4cm là đường ngắn nhất trong các đường kẻ P đến đường thẳng QR.

Vậy chắc chắn có đường xiên PM = 4,5cm (vì PM = 4,5cm > 4cm) kẻ từ P đến đường thẳng QR.

+ Lại có : HM, HR lần lượt là hình chiếu của các đường xiên PM, PR trên đường thẳng QR.

Mà PM < PR ⇒ HM < HR = HQ (đường xiên nào lớn hơn thì hình chiếu lớn hơn).

⇒ M nằm giữa H và Q hoặc H và R

⇒ M nằm trên cạnh QP và có hai điểm M như vậy.