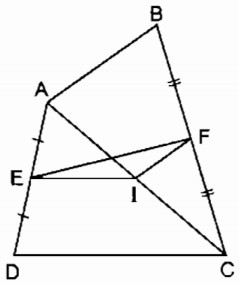
cho tứ giác ABCD .gọi E,F,I theo thứ tự là trung điểm AD,BC,AC.
chứng minh:a)FI//CD,IE//AB
b)EF nhỏ hơn hoặc bằng AB+CD/2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có AE=ED và AI=IC suy ra EI là đường trung bình của tam giác ADC suy ra EI=1/2 DC (1)
BF=FC và AI=IC suy ra IF là đường trung bình của tam giác ABC suy ra IF=1/2AB (2)
xét tam giác EIF có : EF<EI+IF(bất đẳng thức tam giác)
từ (1) và (2) suy ra EF<(AB+CD)/2 (3)
nếu ABCD là hình thang suy ra E,I,F thẳng hàng suy ra ÈF=(AB+CD)/2 (4)
từ (3) và (4) suy ra EF nhỏ hơn hoặc bằng (AB+CD)/2

a: Xét ΔACD có
I là trung điểm của AD
E là trung điểm của AC
Do đó: EI là đường trung bình của ΔACD
Suy ra: EI//CD
Xét ΔACB có
F là trung điểm của BC
E là trung điểm của AC
Do đó: FE là đường trung bình của ΔABC
Suy ra: FE//AB

a) Trong tam giác ADC, ta có:
E là trung điểm của AD (gt)
I là trung điểm của AC (gt)
Nên EI là đường trung bình của ∆ ABC
⇒ EI // CD (tính chất đường trung bình của tam giác)
Và EI=CD/2
Trong tam giác ABC ta có:
I là trung điểm của AC
F là trung điểm của BC
Nên IF là đường trung bình của ∆ ABC
⇒ IF // AB (tính chất đường trung bình của tam giác)
Và IF=AB/2
b) Trong ∆ EIF ta có: EF ≤ EI + IF (dấu “=” xảy ra khi E, I, F thẳng hàng)
Mà EI=\(\dfrac{CD}{2}\); IF=\(\dfrac{AB}{2}\) (chứng minh trên) ⇒EF≤\(\dfrac{CD}{2}+\dfrac{AB}{2}\)
Vậy EF≤\(\dfrac{AB+CD}{2}\) (dấu bằng xảy ra khi AB // CD)
Tick nha 😘
a) Xét ΔACD có
I là trung điểm của AC
E là trung điểm của AD
Do đó: EI là đường trung bình của ΔACD
Suy ra: EI//CD
Xét ΔABC có
I là trung điểm của AC
F là trung điểm của BC
Do đó: IF là đường trung bình của ΔABC
Suy ra: IF//AB

a) Xét tam giác ADC có:
AE = DE (1)
AI = IC (2)
Từ (1) và (2) ⇒ EI là đường trung bình(đtb) của tam giác ADC ⇒ EI // CD
Xét tam giác CBA có:
CF = FB (3)
CI = AI (4)
Từ (3) và (4) ⇒ IF là đtb của tam giác CBA ⇒ IF // AB
b) Xét tam giác EIF có:
EF < IF + EI
Mà: IF = AB/2 ( IF là đtb tam giác CBA )
EI = CD/2 ( EI là đtb tam giác ADC )
⇒ EF < AB/2 + CD/2
⇒ EF < ( AB + CD )/2
Trường hợp dấu "=" xảy ra khi 3 điểm E, I , F thẳng hàng hay tứ giác ABCD là hình thang
⇒ EF ≤ ( AB + CD )/2

EK là đtbinh tam giác => EK=1/2 CD, KF=1/2 AB áp dụng Bđt trong tam giác EKF có EF< EK+KF =>EF< 1/2(AB+CD) . Khi K nằm giữa Evà F thì EF= EK+KF = 1/2(AB+CD) kết hợp cả 2 => đpcm

nâng cao phát triển toán 8 tập 1 bài 16 phần hình, vào đó mà xem mình lười đánh lắm
mình mới học lớp 7