Đáp án A

Chọn trục toạ độ thẳng đứng, chiều dương hướng xuống gốc toạ độ tại vị trí bạn Giang thả ở tầng 19, gốc thời gian lúc bi A rơi.

Phương trình chuyển động của viên bi A: với 

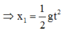
Phương trình chuyển động của viên bi B: với 

thả rơi sau 1s so vói gốc thời gian 

Khi 2 viên bi gặp nhau:

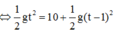
và cách vị trí thả của giang là

= 112,5m

Giải :

Chọn trục toạ độ thẳng đứng, chiều dương hướng xuống gốc toạ độ tại vị trí bạn Giang thả ở tầng 19, gốc thời gian lúc bi A rơi.

Phương trình chuyển động của viên bi A: với  x 01 = 0 m ; v 01 = 0 m / s ⇒ x 1 = 1 2 g t 2

Phương trình chuyển động của viên bi B: với x 02 = 10 m ; v 02 = 0 m / s  thả rơi sau 1s so vói gốc thời gian  x 2 = 10 + 1 2 g ( t − 1 ) 2

Khi 2 viên bi gặp nhau: x 1   =   x 2   ⇔ 1 2 g t 2 = 10 + 1 2 g ( t − 1 ) 2 ⇒ t   =   1 , 5 s  và cách vị trí thả của giang là  x 1 = 1 2 g . t 2 = 1 2 .10.1 , 5 2 = 112 , 5 m

Chiều cao tầng hầm B2 là:

 \(2,7.\frac{4}{3} = \frac{{18}}{5} = 3,6\,\,(m)\)

Chiều cao tầng hầm của toà nhà so với mặt đất là:

 \(2,7 + 3,6 = 6,3\,\,(m)\)

nhưng rõ ràng là bạn viết tòa nhà thứ nhất có 20 tầng và tòa nhà thứ hai thì gấp 15 thi.

gấp 15 là gì????

Tầng trệt, tầng 1 và tầng 2 cao: 1,5 x 3 = 4,5 ( m )

Các tầng còn lại và sân thượng cao: 85 - 4,5 = 80,5 ( m )

Các tầng còn lại là: 80,5 : 1,2 = 67 ( tầng ) dư 0,1 m của sân thượng

Tòa nhà này có: 67 + 3 = 70 ( tầng )             

           Đáp số: 70 tầng

Chọn trục tọa độ thẳng đưgs, chiều dương hướng xuống.

Gốc tọa độ tại vị trí thả viên bi A.

Gốc thời gian là lúc viên bi A rơi.

Ptrình chuyển động:

+ Viên bi A: \(y_1=y_{02}+\dfrac{1}{2}gt^2=\dfrac{1}{2}gt^2\)

+ Viên bi B: \(y_2=y_{02}+\dfrac{1}{2}g\left(t-t_0\right)=10+\dfrac{1}{2}g\left(t-1\right)^2\)

Khi 2 viên bi gặp nhau thì: \(y_1=y_2\)

\(\Leftrightarrow\dfrac{1}{2}gt^2=10+\dfrac{1}{2}g\left(t-1\right)^2\)

\(\Leftrightarrow t=1,5s\)

Vậy.............