Tìm nghiệm của các đa thức sau:
B(x) = 2x + 10 ; b) C(x) = 3x –
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: 2x + 10 = 0 ⇔ 2x = -10 ⇔ x = -10 : 2 ⇔ x = -5
Vậy x = -5 là nghiệm của đa thức 2x + 10

a: Đặt A(x)=0
=>2x+10=0
hay x=-5
b: Đặt B(x)=0
=>-4/3x2+x=0
=>4/3x2-x=0
=>x(4/3x-1)=0
=>x=0 hoặc x=3/4

a. Ta có: 2x + 10 = 0 ⇔ 2x = -10 ⇔ x = -10 : 2 ⇔ x = -5
Vậy x = -5 là nghiệm của đa thức 2x + 10
b. Ta có: 3x - 1/2 = 0 ⇔ 3x = 1/2 ⇔ x = 1/2 : 3 = 1/6
Vậy x = 1/6 là nghiệm của đa thức 3x - 1/2
c. Ta có: x2 – x = 0 ⇔ x(x – 1) = 0 ⇔ x = 0 hoặc x – 1 = 0
⇔ x = 0 hoặc x = 1
Vậy x = 0 và x = 1 là các nghiệm của đa thức x2 – x
a. Ta có: 2x + 10 = 0 ⇔ 2x = -10
⇔ x = -10 : 2
⇔ x = -5 V
ậy x = -5 là nghiệm của đa thức 2x + 10
b. Ta có: 3x - 1/2 = 0 ⇔ 3x = 1/2 ⇔ x = 1/2 : 3 = 1/6
Vậy x = 1/6 là nghiệm của đa thức 3x - 1/2
c.Ta có: x2 – x = 0 ⇔ x(x – 1) = 0 ⇔ x = 0 hoặc x – 1 = 0 ⇔ x = 0 hoặc x = 1
Vậy x = 0 và x = 1 là các nghiệm của đa thức x2 – x

a: 2x+10=0
nên x=-5
b: 3x-1/2=0
=>3x=1/2
hay x=1/6
c: =>x(x-1)=0
=>x=0 hoặc x=1

a: Đặt A(x)=0
=>2x+10=0
hay x=-5
b: Đặt B(x)=0
=>4/3x2-x=0
=>x(4/3x-1)=0
=>x=0 hoặc x=3/4

a)\(2x-5=0\)
\(2x=5\)
\(x=\frac{5}{2}\)
Vậy, \(x=\frac{5}{2}\)là nghiệm của đa thức \(2x-5\)
b) \(x\left(2x+2\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\2x+2=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\2x=-2\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=-1\end{cases}}\)
Vậy \(x=0\)và \(x=-1\)là nghiệm của đa thức \(x\left(2x-2\right)\)
a) Ta có :
2x - 5 = 0
=> 2x = 5
=> x = 5/2
Vậy nghiệm của đa thức 2x - 5 là 5/2
b) x (2x+2) = 0
2 x+ 2 = 0.x
=> 2x +2 = 0
=> 2x = -2
=> x = -1
Vậy nghiệm của đa thức x .(2x +2 ) là -1
Chúc bn hok tốt ạ !!!~~~^-^

`@` `\text {Ans}`
`\downarrow`
`a)`
`6 - 2x=0`
`\Rightarrow 2x = 6-0`
`\Rightarrow 2x=6`
`\Rightarrow x=6/2`
`\Rightarrow x=3`
Vậy, nghiệm của đa thức là `x=3`
`b)`
\(x^{2023}+8x^{2020}?\)
\(x^{2023}+8x^{2020}=0\)
`\Rightarrow `\(x^{2020}\left(x^3+8\right)=0\)
`\Rightarrow `\(\left[{}\begin{matrix}x^{2020}=0\\x^3+8=0\end{matrix}\right.\)
`\Rightarrow `\(\left[{}\begin{matrix}x=0\\x^3=-8\end{matrix}\right.\)
`\Rightarrow `\(\left[{}\begin{matrix}x=0\\x^3=\left(-2\right)^3\end{matrix}\right.\)
`\Rightarrow `\(\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Vậy, nghiệm của đa thức là `x={0;-2}.`
a) Để tìm nghiệm của đa thức 6 - 2x, ta giải phương trình sau: 6 - 2x = 0
Đưa -2x về bên trái và 6 về bên phải: -2x = -6
Chia cả hai vế của phương trình cho -2: x = 3
Vậy nghiệm của đa thức 6 - 2x là x = 3.
b) Để tìm nghiệm của đa thức x^2023 + 8x^2020, ta đặt đa thức bằng 0: x^2023 + 8x^2020 = 0
Chúng ta có thể nhân chung cho x^2020 để thu được: x^2020(x^3 + 8) = 0
Điều này đồng nghĩa với: x^2020 = 0 hoặc x^3 + 8 = 0
Nghiệm của phương trình x^2020 = 0 là x = 0.
Đối với phương trình x^3 + 8 = 0, chúng ta có thể sử dụng công thức Viète để tìm nghiệm. Tuy nhiên, trong trường hợp này, chúng ta có thể nhận thấy rằng phương trình x^3 + 8 = 0 có một nghiệm rõ ràng là x = -2.
Vậy nghiệm của đa thức x^2023 + 8x^2020 là x = 0 và x = -2.

a) Nghiệm của đa thức \(f\left(x\right)=3x-1\)
\(f\left(x\right)=3x-1=0\)
\(\Rightarrow3x=1\)
\(\Rightarrow x=\dfrac{1}{3}\)
Vậy nghiệm của đa thức \(f\left(x\right)\) là \(\dfrac{1}{3}\)
b) Nghiệm của đa thức \(A\left(x\right)=x-\dfrac{1}{2}\)
\(A\left(x\right)=x-\dfrac{1}{2}\)
\(\Rightarrow x=\dfrac{1}{2}\)
Vậy nghiệm của đa thức là \(x=\dfrac{1}{2}\)
c) Nghiệm của đa thức \(B\left(x\right)=-2x+1\)
\(B\left(x\right)=-2x+1=0\)
\(\Rightarrow-2x=-1\)
\(\Rightarrow x=\dfrac{-1}{-2}=\dfrac{1}{2}\)
Vậy nghiệm của đa thức \(x=\dfrac{1}{2}\)
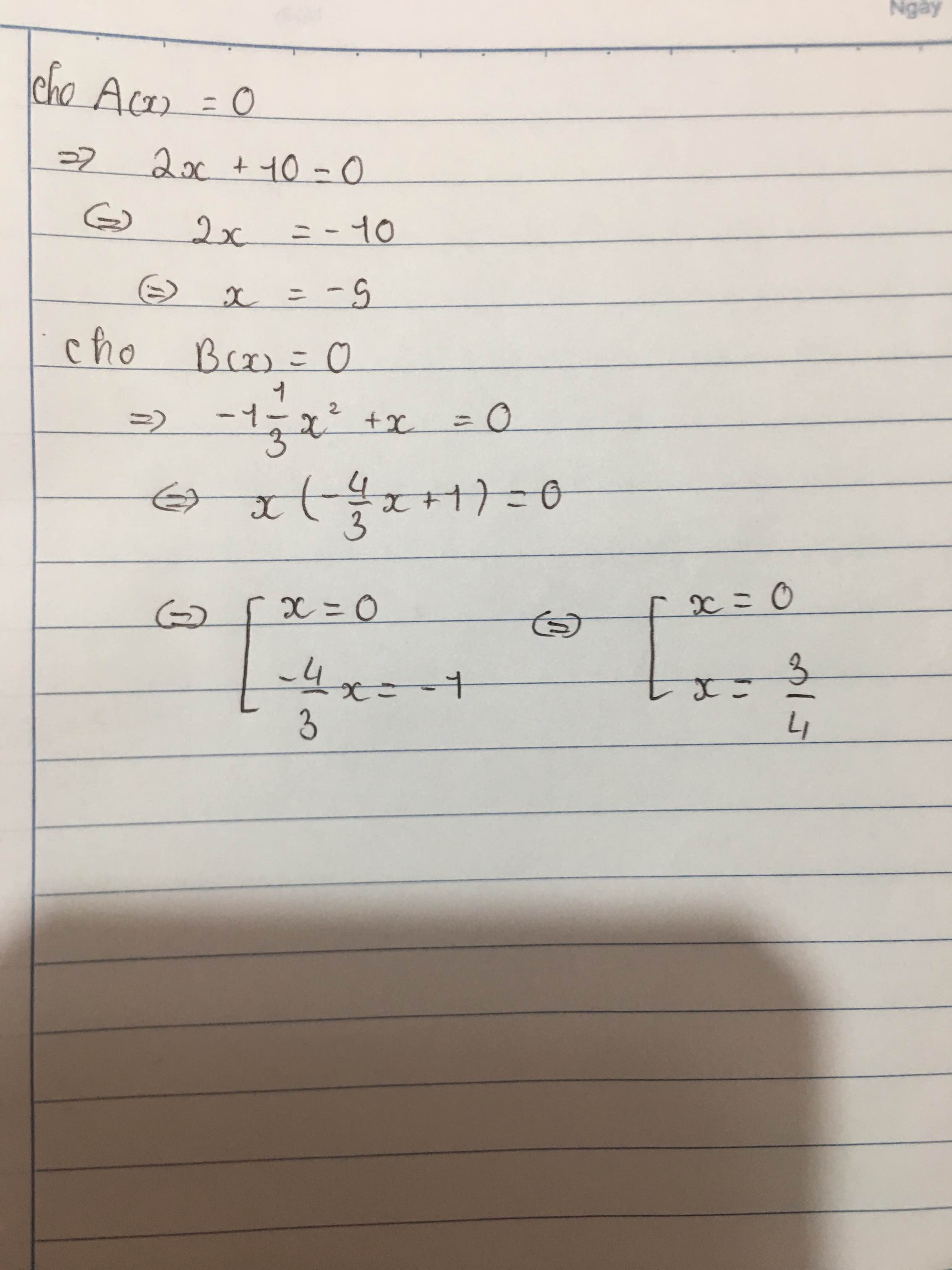
b(x) = 2x+10=0
b(x)= 2x=0+10
b(x)=2x=10
b(x)=10:2=5
vậy x=5 là nghiệm của đa thức b(x)
còn C(x) kìa