cho tam giác abc nhọn nội tiếp đường tròn (O).Các đường cao AK, BI cắt nhau tại H.Gọi D,E,F lần lượt là tâm của các đường tròn ngoại tiếp tam giác AIH,AKC,BKI
a) C/m OEDF là hình bình hành
b) CH cắt AB cắt ở J.Cm:
*AK.BI.CJ=AB.BC.AC.sinBAC.sinACB.sinCBA
*AK.BI.CJ=AB.BC.AC.cóCAK.cosABI.cosBAC
c)C/m sinABC.sinACB-cosABC.cosACB=cosBAC
d)Cho biết BAC=60,AB=30mm,BC=15 căn 6.Hãy giải tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét Δ AFH vuông tại F => A, F, H thuộc đường tròn đường kính AH
ΔAGH vuông tại G => A, G, H thuộn đường tròn đường kính AH
=> Tứ giác AFHG nội tiếp đường tròn đường kính AH
CMTT => BGFC nội tiếp đường tròn đường kính BC
b) Do I là tâm đường tròn ngoại tiếp tứ giác AFHG => I là trung điểm AH
M là tâm đường tròn ngoại tiếp tứ giác BGFC => M là trrung điểm BC
Xét ΔAHG vuông tại G, trung tuyến GI => GI = IA = IH => ΔIAG cân tại I => \(\widehat{IAG}=\widehat{IGA}\)
CMTT => \(\widehat{MCG}=\widehat{MGC}\). Mà \(\widehat{MCG}=\widehat{IAG}\) (cùng phụ \(\widehat{GBC}\)) => \(\widehat{MGC}=\widehat{IGA}\)
=> \(\widehat{IGA}+\widehat{IGH}=\widehat{MGC}+\widehat{IGH}=\widehat{IGM}=90^o\) => IG ⊥ MG
=> MG là tiếp tuyến đường tròn tâm I
c) Kẻ đường kính AK của đường tròn (O) => \(\widehat{ACK}=90^o\) (góc nội tiếp chắn nửa đường tròn) => ΔACK vuông tại C => \(\widehat{KAC}=90^o-\widehat{AKC}\)
ΔABE vuông tại E => \(\widehat{EAB}=90^o-\widehat{ABE}\) hay \(\widehat{DAB}=90^o-\widehat{ABC}\)
Xét đường tròn (O) có \(\widehat{ABC}=\widehat{AKC}\) (cùng chắn \(\stackrel\frown{AC}\))
=> \(90^o-\widehat{AKC}=90^o-\widehat{ABC}\) => \(\widehat{DAB}=\widehat{KAC}\) => \(\stackrel\frown{BD}=\stackrel\frown{KC}\) (góc nội tiếp bằng nhau chắn các cung bằng nhau)
=> BD = KC (hai cung bằng nhau căng hai dây bằng nhau)
Xét ΔAKC vuông tại C, theo định lý Pytago có: AC2 + KC2 = AK2
Xét ΔAEC vuông tại E, theo định lý Pytago có: EA2 + EC2 = AC2
ΔBED vuông tại E, theo định lý Pytago có: EB2 + ED2 = BD2
Mà BD = KC (cmt) => BD2 = KC2 => EB2 + ED2 = KC2
=> EA2 + EB2 + EC2 + ED2 = AC2 + KC2 = AK2 = (2R)2 = 4R2

a. Ta thấy \(\widehat{HDC}=\widehat{HEC}=90^o\) nên CDHE là tứ giác nội tiếp đường tròn đường kính HC.
b. Ta thấy ngay \(\widehat{IAC}=\widehat{KBC}\) (Cùng phụ với góc ACB) nên \(\widebat{IC}=\widebat{KC}\) (Góc nội tiếp)
suy ra IC = KC ( Liên hệ giữa cung và dây)
Vậy nên tam giác IKC cân tại C.
c. Do \(\widebat{IC}=\widebat{KC}\) nên \(\widehat{KAC}=\widehat{ACI}\) (Góc nội tiếp)
Xét tam giác AHK có AE vừa là đường cao, vừa là phân giác nên AHK là tam giác cân tại A, hay AH = AK.
d. Ta thấy do BOF là đường kính nên \(\widehat{BCF}=90^o\Rightarrow\) AH // FC (Cùng vuông góc với BC).
Tương tự AF // HC vì cùng vuông góc với AB. Vậy thì AFCH là hình bình hành hay AC giao FH tại trung điểm mỗi đường.
P là trung điểm AC nên F cũng là trung điểm FH. Vậy F, H, P thẳng hàng.


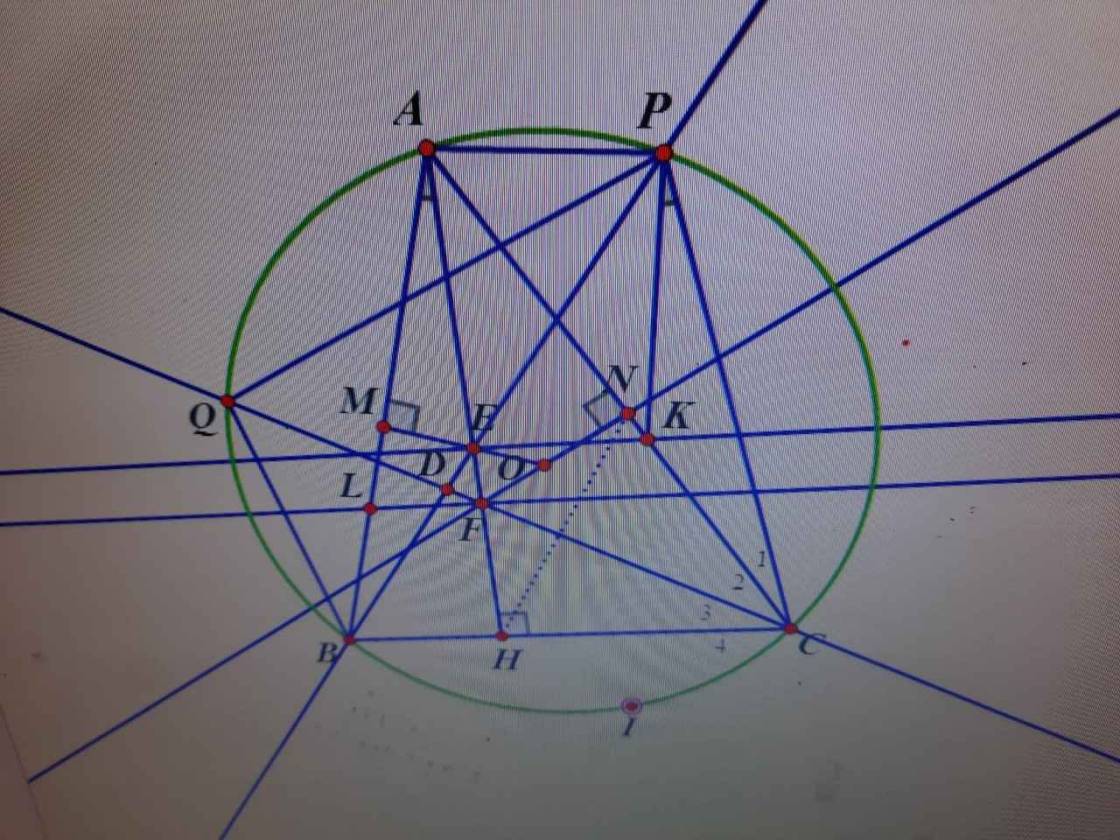
Các bạn giúp mình với