) Gọi 2 góc so le trong là ABC và BCD, Bx và Cy là phân giác của ABC và BCD => ABC = BCD => ABC/2 = BCD/2 => xBC = BCy

Do đó Bx song song Cy

2)a)Từ B kẻ Bz song song Ax => Bz song song Cy

Ta có xAB = ABz và yBC = zBC

Do đó ABC = xAB + yBC = A + C

b) Kẻ Bz song song Ax => ABz = A

Mà ABC = A + C nên zBC = C => Bz song song Cy

Do đó Ax song song Cy

Giúp mìnk vs nha các bn !

các đường thẳng và góc , được biểu diễn trên hình vẽ : 

Kẻ AH ; BK vuông góc với đường thẳng a;b

Xét tam giác vuông ABH có : B₂+BAH =90⁰

lại có góc BAH +A₄=90⁰(do AH vuông góc với a)

=> góc A₄=B₂ ; 2 góc này ở vị trí SLT

Ta có góc :A₂=A₄ ( đối đỉnh ) => góc A₂=B₂ ; 2 góc này ở vị trí đồng vị 

Ta có góc : A₂+A₁=180⁰ => chúng bù nhau 

+) Từ 1 cặp SLT bằng nhau A₄=B₂ ta suy ra được các cặp góc SLT ; đồng vị còn lại bằng nhau , trong phía cùng bù nhau 

Mình nghĩ thế này , mà nói em mới đúng do mình mới học lớp 6 ò , mình mới coi qua vài bài hình lớp 7 , sai thì thôi nha 

a: Xét ΔOAI và ΔOBI có

OA=OB

\(\widehat{AOI}=\widehat{BOI}\)

OI chung

Do đó: ΔOAI=ΔOBI

b: Ta có: ΔOAI=ΔOBI

=>IA=IB

=>I nằm trên đường trung trực của AB(1)

Ta có: OA=OB

=>O nằm trên đường trung trực của AB(2)

Từ (1) và (2) suy ra OI là đường trung trực của BA

=>OI\(\perp\)AB

=>Oz\(\perp\)AB

c: ta có: Oz\(\perp\)AB

AB//CD

Do đó: Oz\(\perp\)CD tại I

Xét ΔOCD có

OI là đường cao

OI là đường phân giác

Do đó;ΔOCD cân tại O

Ta có: ΔOCD cân tại O

mà OI là đường cao

nên I là trung điểm của CD

d: Ta có: OB+BD=OD

OA+AC=OC

mà OB=OA

và OC=OD

nên BD=AC

Xét ΔBDC và ΔACD có

BD=AC

\(\widehat{BDC}=\widehat{ACD}\)(ΔOCD cân tại O)

CD chung

Do đó: ΔBDC=ΔACD

=>\(\widehat{BCD}=\widehat{ADC}\)

=>\(\widehat{MCD}=\widehat{MDC}\)

Xét ΔMCD có \(\widehat{MCD}=\widehat{MDC}\)

nên ΔMCD cân tại M

=>MC=MD

=>M nằm trên đường trung trực của CD(3)

Ta có: ΔOCD cân tại O

mà OI là đường cao

nên OI là đường trung trực của CD(4)

Từ (3) và (4) suy ra O,M,I thẳng hàng

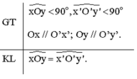
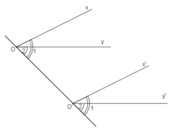
Chứng minh:

Vẽ đường thẳng OO’

Vì Ox // O’x’ nên hai góc đồng vị ∠(O1) và ∠(O'1) bằng nhau

Suy ra: ∠(O1) = ∠(O'1 ) (1)

Vì Oy // O’y’ nên hai góc đồng vị ∠(O2) và ∠(O'2) bằng nhau

Suy ra: ∠(O2) = ∠(O'2)(2)

Từ (1) và (2) suy ra: ∠(O1) - ∠(O2) =∠(O'1) - ∠(O'2)

Vậy ∠(xOy) = ∠(x'O'y')

a) AB//Ox => góc BAO=góc AOC(2 góc so le trong)

AC//Oy => góc CAO=góc AOB (2 góc so le trong)

b)góc BAO=góc AOC;góc CAO=góc AOB mà góc AOC=góc AOB(A thuộc tia phân giác góc BOC)

=>góc BAO=góc CAO =>AO là tia phân giác góc BAC