cho tam giác ABC vuông tại A(AC>AB).Kẻ tia phân giác của góc B cắt cạnh AC tại E từ C hạ đoạn thẳng CD vuông góc với tia phân giác BE (D thuộc BE).Chứng minh rằng:
a, góc AEB=góc DCB
b,EC.AE=ED.BE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 4 2023
a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
góc ABE=góc DBE
=>ΔBAE=ΔBDE
b: BA=BD
EA=ED
=>BE là trung trực của AD
c: góc BAD+góc CAD=90 độ
góc HAD+góc BDA+90 độ
góc BAD=góc BDA
=>góc CAD=góc HAD
=>AD làphân giác của góc HAC
13 tháng 6 2023
a: Xét ΔAEF có
AM vừa là đường cao, vừa là phân giác
=>ΔAEF cân tại A
b:Kẻ BH//CF
=>góc BHE=góc AFE
=>góc BHE=góc BEH
=>BH=BE
Xét ΔMHB và ΔMFC có
góc MBH=góc MCF
MB=MC
góc BMH=góc CMF
=>ΔMHB=ΔMFC
=>BH=CF=BE
DA
24 tháng 5 2021
Giải
a, Vì ED \(\perp\)BC ( gt ) \(\Rightarrow\)\(\Delta\)DBE là tam giác vuông tại D
Xét \(\Delta\) vuông ABE và \(\Delta\)vuông DBE, có :
BE : cạnh chung
góc ABE = góc DBE ( BE là tpg góc ABC )
\(\Rightarrow\)\(\Delta\)vuông ABE = \(\Delta\) vuông DBE ( cạnh huyền góc nhọn )
b, Vì \(\Delta\) ABE = \(\Delta\)DBE ( cmt )
\(\Rightarrow\)BA = BD ( 2 cạnh tương ứng ) \(\Rightarrow\)B nằm trên đtt của AD ( đ/l đảo )
AE = DE ( 2 cạnh tương ứng )\(\Rightarrow\) E nằm trên đtt của AD ( đ/l đảo )
Từ 2 điều trên \(\Rightarrow\) BE là đtt của đoạn thẳng AD
c, +, ta có : \(\Delta\)BAD cân tại B ( BA = BD )
\(\Rightarrow\)góc BAD = góc BDA ( t/c )
Vì AH \(\perp\) BC tại H ( gt ) \(\Rightarrow\) \(\Delta\) HAD vuông tại H
Xét \(\Delta\)vuông HAD, có :
góc HAD + góc HDA ( hay góc BDA ) = 90o ( 2 góc phụ nhau )
Xét \(\Delta\) vuông ABC, có :
góc CAD + góc BAD = 90o ( 2 góc phụ nhau )
Mà góc BDA = góc BAD ( cmt )
Từ các điều trên \(\Rightarrow\)góc HAD = góc CAD (1)
Mà tia AD nằm giữa 2 tia AH, AC ( cách vẽ ) (2)
Từ (1) và (2) \(\Rightarrow\) AD là tpg của góc HAC ( đpcm )
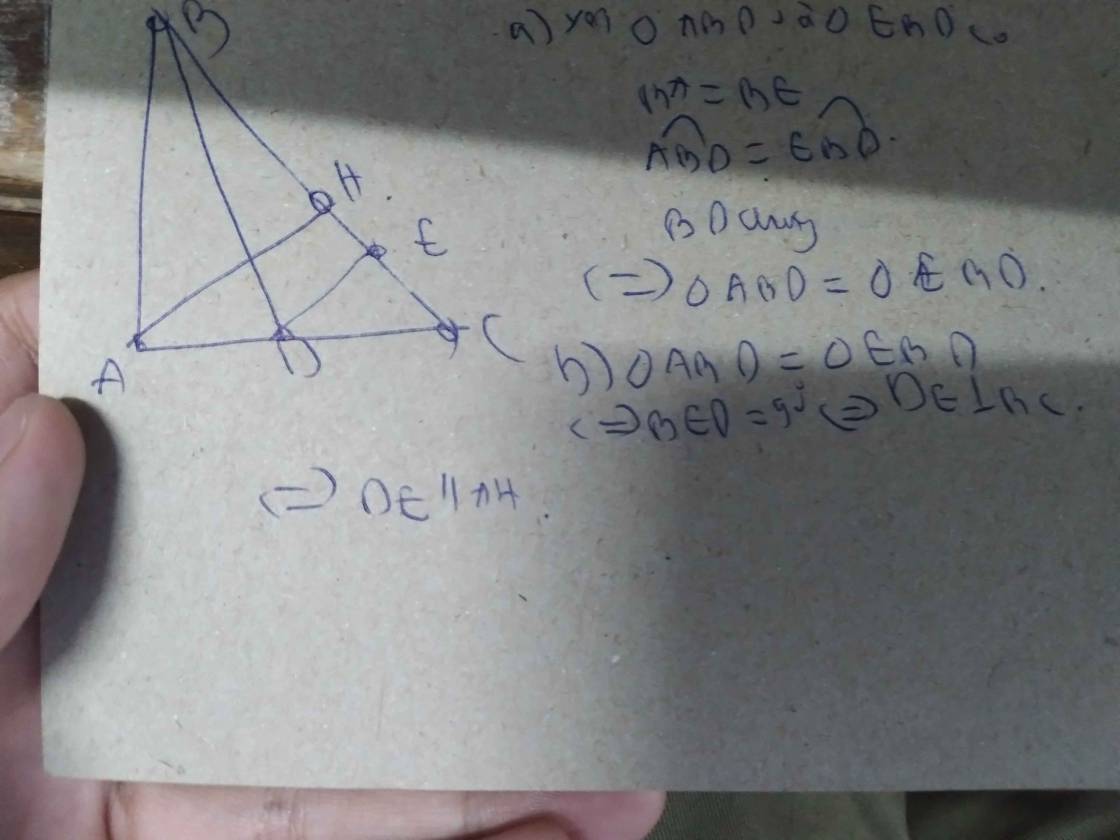
a: Xét ΔABE vuông tại A và ΔDBC vuông tại D có
góc ABE=góc DBC
=>ΔABE đồng dạng với ΔDBC
=>góc AEB=góc DCB
b: Xét ΔEAB vuông tại A và ΔEDC vuông tại D có
góc AEB=góc DEC
=>ΔEAB đồng dạng với ΔEDC
=>EA/ED=EB/EC
=>EA*EC=ED*EB