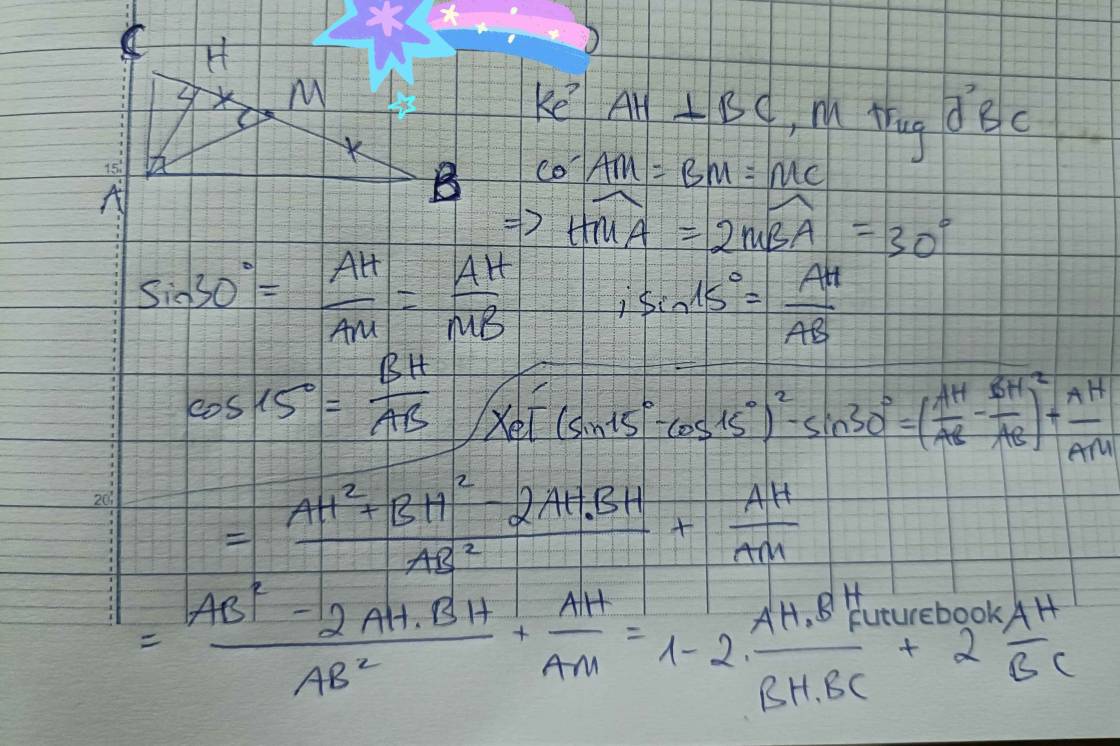
Cho tam giác ABC có góc A=90 độ, góc ABC=15 độ, Chứng minh rằng: BC2=4AB.AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



=> \(\widehat{C}=180-90-15=70^o\)
Ta có:
\(sin15=\dfrac{AC}{BC}\Rightarrow BC=\dfrac{AC}{sin15}=\dfrac{4AC}{\sqrt{6}-\sqrt{2}}\)
\(sin75=\dfrac{AB}{BC}\Rightarrow BC=\dfrac{AB}{sin75}=\dfrac{4AB}{\sqrt{6}+\sqrt{2}}\)
\(\Rightarrow BC^2=\dfrac{16.AB.AC}{\left(\sqrt{6}+\sqrt{2}\right)\left(\sqrt{6}-\sqrt{2}\right)}=4.AB.AC\)

Ta có tính chất: Trong tam giác vuông, cạnh đối diện với góc 300 thì bằng 1 nửa cạnh huyển
Ở đề bài ta có: BC = 2AC
=> \(\widehat{ABC}=30^0\)
Ta lại có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)( định lí tổng ba góc trong một tam giác)
=> \(\widehat{ACB}=180^0-30^0=60^0\)
Vậy góc ACB = 600

Ta có tam giác ABC = 90 độ nên
góc ABC +góc ACB = 90 độ
vì lấy điểm E nằm trong tam giác nên
góc ABE + EBC + ACE + ECB = 90 độ
=> góc EBC + ECB < 90 độ
nên góc BEC > 90 độ

Vẽ đường thẳng song song với AC và vuông góc với AB tài D và N ( góc NDA = 90 độ)
Xét tam giác NAD và tam giác NAH có :
góc DAN = góc NAH ( vì DN là tia p/g góc BAH)
AN cạnh chung
=> tam giác NAD = tam giác NAH ( ch-gn)
=> góc DNA = góc ANH ( hai góc tương ứng ) (1)
Mặt khác : góc DNA = góc NAC ( hai góc so le trong )
Kết hợp (1) => góc DNA = góc ANH = góc NAC => tam giác NCA cân tại C => NC =AC (3)
Xét tam giác NCI và tam giác ACI có:
NC =AC ( do (3))
CI cạnh chung
góc NCI = góc ICA ( CI là p/g góc BCA)
=> tam giác NCI = tam giác ACI ( c.g.c)
=> góc NIC = góc AIC ( hai góc tương ứng )
Mà góc NIC và góc AIC là cặp góc kề bù
=> góc NIC = góc AIC = 90 độ
**** bạn

Ta có hình vẽ:
Vì AI là phân giác của BAH nên \(BAI=HAI=\frac{BAH}{2}\)
CI là phân giác của BCA nên \(BCI=ACI=\frac{BCA}{2}\)
Δ ABC vuông tại A có: ABC + BCA = 90o
=> BCA = 90o - ABC
=> \(\frac{BCA}{2}=45^o-\frac{ABC}{2}=ACI\)
Δ ABH vuông tại H có: ABH + BAH = 90o
=> BAH = 90o - ABH
=> \(\frac{BAH}{2}=45^o-\frac{ABH}{2}=BAI\)
Lại có: IAC = BAC - BAI
=> IAC = 90o - (45o - \(\frac{ABH}{2}\))
=> IAC = 45o + \(\frac{ABH}{2}\)
Xét Δ AIC có: AIC + IAC + ICA = 180o (tổng 3 góc của Δ)
=> AIC + 45o + \(\frac{ABH}{2}\) + 45o - \(\frac{ABC}{2}\) = 180o
=> AIC + 90o = 180o
=> AIC = 180o - 90o = 90o (đpcm)