Giúp mình câu này đi mình cần gấp 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


uses crt;
var st:string;
d,i:integer;
begin
clrscr;
readln(st);
d:=length(st);
for i:=1 to d do
if (st[i] in ['0'..'9']) then write(st[i]);
readln;
end.


Phương trình tương đương
\(\left[{}\begin{matrix}x=\dfrac{5\pi}{12}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\end{matrix}\right.,k\in Z\)
Xét họ nghiệm \(x=\dfrac{5\pi}{12}+k\pi,k\in Z\).
Do \(-\dfrac{\pi}{2}< \dfrac{5\pi}{12}+k\pi< \dfrac{8\pi}{3}\) nên \(-\dfrac{11\pi}{12}< k\pi< \dfrac{9\pi}{4}\)
⇒ \(-\dfrac{11}{12}< k< \dfrac{9}{4}\). Mà k ∈ Z nên k ∈ {0 ; 1}
Vậy các nghiệm thỏa mãn phương trình là các phần tử của tập hợp :
S1 = \(\left\{\dfrac{5\pi}{12};\dfrac{17\pi}{12}\right\}\)
Xét họ nghiệm \(x=-\dfrac{\pi}{4}+k\pi\) với k ∈ Z.
Do \(-\dfrac{\pi}{2}< \dfrac{-\pi}{4}+k\pi< \dfrac{8\pi}{3}\) nên \(-\dfrac{\pi}{4}< k\pi< \dfrac{35\pi}{12}\)
nên \(-\dfrac{1}{4}< k< \dfrac{35}{12}\). Mà k ∈ Z nên k∈ {0 ; 1 ; 2}
Vậy các nghiệm thỏa mãn phương trình là các phần tử của tập hợp
S2 = \(\left\{-\dfrac{\pi}{4};\dfrac{3\pi}{4};\dfrac{7\pi}{4}\right\}\)
Vậy các nghiệm thỏa mãn phương trình là các phần tử của tập hợp
S = S1 \(\cup\) S2 = \(\left\{\dfrac{5\pi}{12};\dfrac{17\pi}{12};-\dfrac{\pi}{4};\dfrac{3\pi}{4};\dfrac{7\pi}{4}\right\}\)

a: \(\widehat{\left(SC;\left(ABCD\right)\right)}=\widehat{CS;CA}=\widehat{SCA}\)
Ta có: SA\(\perp\)(ABCD)
=>SA\(\perp\)AC
=>ΔSAC vuông tại A
Vì ABCD là hình vuông
nên \(AC=AD\cdot\sqrt{2}=a\sqrt{2}\)
Xét ΔSAC vuông tại A có \(tanSCA=\dfrac{SA}{AC}=\dfrac{a\sqrt{6}}{a\sqrt{2}}=\sqrt{3}\)
nên \(\widehat{SCA}=60^0\)
=>\(\widehat{SC;\left(ABCD\right)}=60^0\)
b: Ta có: BD\(\perp\)AC
BD\(\perp\)SA
SA,AC cùng thuộc mp(SAC)
Do đó: BD\(\perp\)(SAC)
\(\widehat{SB;\left(SAC\right)}=\widehat{SB;SD}=\widehat{BSD}\)
Vì ABCD là hình vuông
nên \(AC=BD=a\sqrt{2}\)
ΔSAD vuông tại A
=>\(SA^2+AD^2=SD^2\)
=>\(SD^2=\left(a\sqrt{6}\right)^2+a^2=7a^2\)
=>\(SD=a\sqrt{7}\)
ΔSAB vuông tại A
=>\(SA^2+AB^2=SB^2\)
=>\(SB=a\sqrt{7}\)
Xét ΔSBD có \(cosBSD=\dfrac{SB^2+SD^2-BD^2}{2\cdot SB\cdot SD}\)
\(=\dfrac{7a^2+7a^2-2a^2}{2\cdot a\sqrt{7}\cdot a\sqrt{7}}=\dfrac{6}{7}\)
=>\(sinBSD=\sqrt{1-\left(\dfrac{6}{7}\right)^2}=\dfrac{\sqrt{13}}{7}\)
=>\(\widehat{BSD}\simeq31^0\)
=>\(\widehat{SB;\left(SAC\right)}\simeq31^0\)

\(\left(x-3\right)^{30}=\left(x-3\right)^{10}\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\\x=4\end{matrix}\right.\)


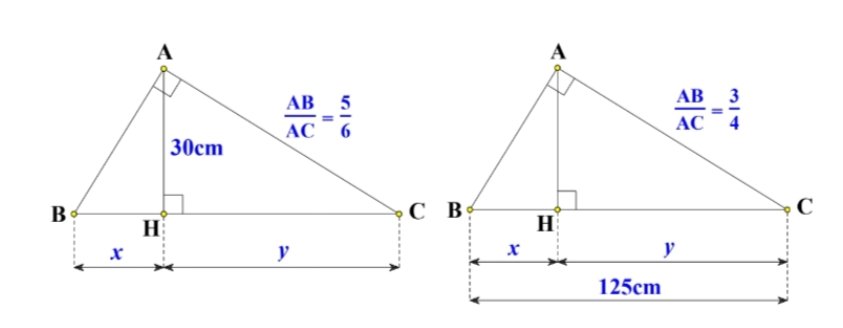
a: AB/AC=5/6
=>HB/HC=25/36
=>HB/25=HC/36=k
=>HB=25k; HC=36k
AH^2=HB*HC
=>25k*36k=30^2
=>900k^2=900
=>k=1
=>x=25cm; y=25cm
b: AB/AC=3/4
=>HB/HC=9/16
=>x/y=9/16
=>x/9=y/16=(x+y)/(9+16)=125/25=5
=>x=45cm; y=80cm

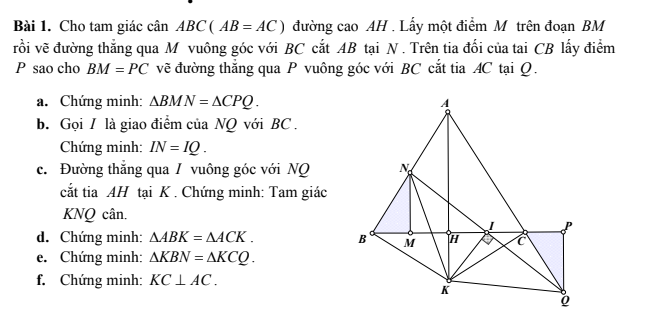
a, Vì tam giác ABC cân tại A nên \(\widehat{NBM}=\widehat{ACB}\)
Mà \(\widehat{ACB}=\widehat{PCQ}\left(đối.đỉnh\right)\Rightarrow\widehat{NBM}=\widehat{PCQ}\)
Mà \(\widehat{NMB}=\widehat{CPQ}=90^0;BM=PC\)
Do đó \(\Delta BMN=\Delta CPQ\left(g.c.g\right)\)
b, Vì \(BM//PQ\left(\perp BP\right)\) nên \(\widehat{MNI}=\widehat{IQP}\)
Mà \(\widehat{NMI}=\widehat{IPQ}=90^0;MN=PQ\left(\Delta BMN=\Delta CPQ\right)\)
Do đó \(\Delta IMN=\Delta IPQ\left(g.c.g\right)\)
\(\Rightarrow IN=IQ\)
c, Vì IK là đường cao cũng là trung tuyến tam giác KNQ nên tam giác KNQ cân tại K

b. - Trích mỗi chất một ít làm mẫu thử.
| Na2O | P2O5 | MgO | |
| Qùy tím ẩm | Hóa xanh | Hóa đỏ | Không đổi màu |
PTHH:
\(Na_2O+H_2O\rightarrow2NaOH\\ P_2O_5+3H_2O\rightarrow2H_3PO_4\)
e.Dùng que diêm :
+Nếu cho diêm vào mà không có lửa thì đó là khí CO2
+Cho tàn đóm lửa của que diêm vào bình nếu bùng cháy là có khi Oxi
+Nếu như lửa trong bình khí đó cháy càng ngày càng to và bắt đầu chuyển sang màu xanh nhạt thì đó chính là khí Hidro





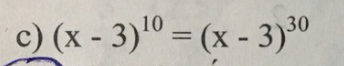 giúp mình câu này với mình đang cần gấp
giúp mình câu này với mình đang cần gấp

đăng nên nói cần câu nào e nhé!
Bài 6:
-Thay \(x=1\) vào \(f\left(x\right)=x\left(x+1\right)+\left(x+1\right)\left(x+2\right)+...+\left(x+49\right)\left(x+50\right)\), ta được:
\(f\left(1\right)=1\left(1+1\right)+\left(1+1\right)\left(1+2\right)+...+\left(1+49\right)\left(1+50\right)\)
\(=1.2+2.3+...+50.51\)
\(=\dfrac{1.2.3+2.3.3+...+50.51.3}{3}\)
\(=\dfrac{1.2.3+2.3.\left(4-1\right)+...+50.51.\left(52-49\right)}{3}\)
\(=\dfrac{1.2.3+2.3.4-1.2.3+...+50.51.52-49.50.51}{3}\)
\(=\dfrac{50.51.52}{3}=44200\)