Trong 1 hình tròn có diện tích S lấy 2017 điểm bất kì. C/m ít nhất có 3 điểm tạo thành 1 tam giác mà diện tích S< S/1008
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi d là khoảng cách Ai AJ là 2 điểm xa nhau nhất trong các điểm thuộc tập S
Giả sử Ak là điểm xa đường Ai AJ nhất. Ta có tam giác Ai AJAk có diện tích không lớn hơn 1(theo giả thiết). và là tam giác có Smax
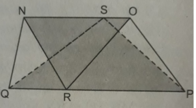
Từ các đỉnh Ai, AJ,Ak ta kẻ các đường thẳng song song với các cạnh của tam giác.
Ta sẽ thu được 4 tam giác con bằng nhau và tam giac lớn nhất
Diện tích tam giác lớn nhất này không quá 4 đơn vị
Tam giác lớn nhất này chứa cả 8065 điểm đã cho
(dễ chứng minh bằng phản chứng vì S của tam giác Ai AJAmax)
Vì
8065:4=2016 dư 1
Suy ra tồn tại 1 trong 4 tam giác con chứa không dưới 2017 điểm thuộc tập S thỏa mãn đề bài.

Ta có:
x + 1/2 + √(x + 1/4)
= x + 1/4 + √(x + 1/4) + 1/4
= (√(x + 1/4) + 1/2)^2
=> PT <=> x + |√(x + 1/4) + 1/2| = 2
Làm nốt

Do số điểm là hữu hạn nên số tam giác tạo ra hữu hạn
Giả sử \(S_{MNP}\)lớn nhất
qua M,N,P kể các đường song song với cạnh đối diện chúng cắt nhau tại ABC khi đó
\(S_{ABC}\le4S_{MNP}\le4\)
ta CM 2009 điểm đã cho thuộc tam giác ABC
Giả sử co điểm D ở ngoài tam giác ABC khi đó \(S_{MNP}< S_{DMN}\) vô lí
Tìm giá trị của x để biểu thức P= \(\frac{x^2-x+1}{\left(x-1\right)^2}\) đạt giá trị nhỏ nhất