Ông A vay ngắn hạn ngân hàng 100 triệu đồng, với lãi suất 12%/năm. Ông muốn hoàn nợ cho ngân hàng theo cách : Sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi lần là như nhau và trả hết tiền nợ sau đúng 3 tháng kể từ ngày vay. Hỏi, theo cách đó, số tiền m mà ông A sẽ phải trả cho ngân hàng trong mỗi lần hoàn nợ là bao nhiêu ? Biết rằng, lãi suất ngân hàng không thay đổi trong thời gian ông A hoàn nợ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Số tiền ông A còn nợ ngân hàng sau lần trả thứ nhất:
(100 + 100. 0,01) – m = 100.1,01 – m (triệu đồng)
Số tiền ông A còn nợ ngân hàng sau lần trả thứ hai:
(100 + 1,01 - m) .1,01 – m = 100.1,012 - (1,01 + 1) m (triệu đồng)
Vì ông A đã hoàn cho ngân hàng toàn bộ số tiền nợ , sau lần trả thứ ba, nên
0 = [ 100.1,012 - (1,01 + 1)m] .1,01 - m= 100.1,013 - [ 1,012 + 1,01 + 1]m
Từ đó suy ra
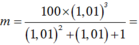
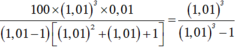

Đáp án B
Áp dụng CT trả góp ta có m = 100 1 + 12 % 12 12 12 % 12 1 + 12 % 12 12 − 1 ≈ 0 , 885 triệu đồng

Chọn D
Vay vốn trả góp: Vay ngân hàng số tiền là P đồng với lãi suất r% trên tháng. Sau đúng một tháng kể từ ngày vay, bắt đầu hoàn nợ; hai lần hoàn nợ cách nhau đúng một tháng, mỗi tháng hoàn nợ số tiền là X đồng và trả hết số tiền nợ sau đúng n tháng





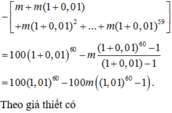
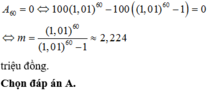
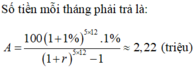
Đây là câu 21 của đề minh họa thị THPT QG 2017.
Lãi suất 12%/năm => lãi suất 1%/tháng.
Nếu còn nợ a đồng thì phải trả lãi 0,01 a cho 1 tháng.
Sau tháng đầu tiên, sau khi trả m đồng thì ông A còn nợ là:
(a + 0,01.a) - m = a. 1,01 - m
Sau tháng thứ hai, sau khi trả tiếp m đồng thì ông A còn nợ là:
(a . 1,01 - m) . 1,01 - m
Sau tháng thứ ba, sau khi trả tiếp m đồng thì ông A còn nợ là:
[(a. 1,01 - m) . 1,01 - m] . 1,01 - m
Con số nợ cuối cùng này phải bằng 0, suy ra:
[(a. 1,01 - m) . 1,01 - m] . 1,01 - m = 0
=> \(m=\frac{a.1,01^3}{1,01^2+1,01+1}=\frac{a.1,01^3\left(1,01-1\right)}{1,01^3-1}=\frac{a.1,01^3.0,01}{1,01^3-1}\)
Thay a = 100 vào ta có:
\(m=\frac{1,01^3}{1,01^3-1}\)