Mình cần gấp lắm , giải thích từ từ hộ mìnhCho hình chóp S.ABC có đáy là tam giác ABC vuông tại B, Có AB = a, AC = 2a và cạnh bên SA vuông góc với đáy. Biết góc giữa hai mặt phẳng (SBC) và (ABC) bằng 60 độ .1) Tính góc giữa SC và mặt phẳng (ABC).2) Tính theo a khoảng cách từ là trọng tâm G của tam giác SAB đến mặt phẳng...
Đọc tiếp
Mình cần gấp lắm , giải thích từ từ hộ mình
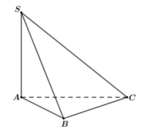
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B, Có AB = a, AC = 2a và cạnh bên SA vuông góc với đáy. Biết góc giữa hai mặt phẳng (SBC) và (ABC) bằng 60 độ .
1) Tính góc giữa SC và mặt phẳng (ABC).
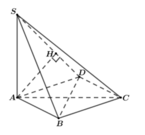
2) Tính theo a khoảng cách từ là trọng tâm G của tam giác SAB đến mặt phẳng (SBC).
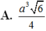
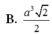
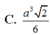
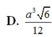
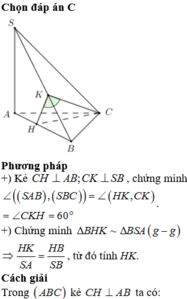
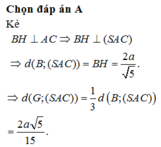
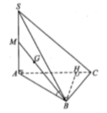
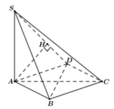
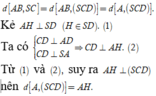
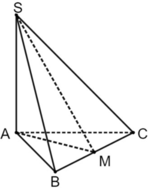
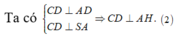
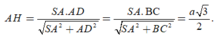
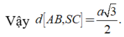
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Mà \(\left\{{}\begin{matrix}BC=\left(SBC\right)\cap\left(ABC\right)\\SB=\left(SAB\right)\cap\left(SBC\right)\\AB=\left(SAB\right)\cap\left(ABC\right)\end{matrix}\right.\) \(\Rightarrow\widehat{SBA}\) là góc giữa (SBC) và (ABC)
\(\Rightarrow\widehat{SBA}=60^0\Rightarrow SA=AB.tan60^0=a\sqrt{3}\)
\(SA\perp\left(ABC\right)\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABC)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=\dfrac{\sqrt{3}}{2}\Rightarrow\widehat{SCA}\approx40^053'\)
Gọi M là trung điểm SB \(\Rightarrow GM=\dfrac{1}{3}AM\) (tính chất trọng tâm)
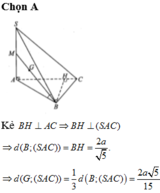
\(\Rightarrow d\left(G;\left(SBC\right)\right)=\dfrac{1}{3}d\left(A;\left(SBC\right)\right)\)
Từ A kẻ \(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH=d\left(A;\left(SBC\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}=\dfrac{1}{3a^2}+\dfrac{1}{a^2}=\dfrac{4}{3a^2}\Rightarrow AH=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow d\left(G;\left(SBC\right)\right)=\dfrac{1}{3}AH=\dfrac{a\sqrt{3}}{6}\)