Cho tam giác ABC, kẻ BD vuông góc vs AC, Kẻ CE vuông góc vs AC, Trên tia đối của BD lấy H sao cho BH=AC. Trên tia đối của CE lấy K sao cho CK=AB. CMR : AH=AK
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Có \(\widehat{ABD}+\widehat{A}=\widehat{A}+\widehat{ACE}=90^0\)
\(\Rightarrow\widehat{ABD}=\widehat{ACE}\)
\(\Rightarrow180^0-\widehat{ABD}=180^0-\widehat{ACE}\)
\(\Leftrightarrow\widehat{ABH}=\widehat{ACK}\)
Xét tam giác ABH và tam giác ACK có:
\(AB=CK\)
\(\widehat{ABH}=\widehat{ACK}\)
\(HB=AC\)
nên tam giác ABH= tam giác KCA (c.g.c)
\(\Rightarrow AH=AK\)

Giải:
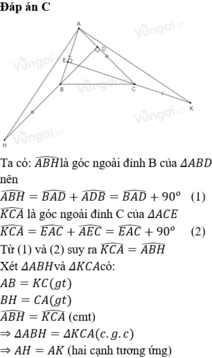
Ta có: ACKˆ=Aˆ+AECˆ=Aˆ+90oACK^=A^+AEC^=A^+90o ( t/c góc ngoài )
ABHˆ=Aˆ+ADBˆ=Aˆ+90oABH^=A^+ADB^=A^+90o ( t/c góc ngoài )
⇒ACKˆ=ABHˆ⇒ACK^=ABH^
Xét ΔABH,ΔKCAΔABH,ΔKCA có:
BH = CA ( gt )
ABHˆ=KCAˆ(cmt)ABH^=KCA^(cmt)
AB = CK ( gt )
⇒ΔABH=ΔKCA(c−g−c)⇒ΔABH=ΔKCA(c−g−c)
⇒AH=AK⇒AH=AK ( cạnh t/ứng ) ( đpcm )
Vậy...
ABCDHKE
Giải:
Ta có: gócACK=gócA+gócAEC=gócA+90 độ gócACK=gócA+gócAEC=gócA+90độ ( t/c góc ngoài )
gócABH=gócA+gócADB=gócA+90độ gócABH=gócA+gócADB=gócA+90độ ( t/c góc ngoài )
⇒gócACK=gócABH⇒gócACK=gócABH
Xét ΔABH,ΔKCAΔABH,ΔKCA có:
BH = CA ( gt )
gócABH=gócKCA (cmt) góc ABH=góc KCA(cmt)
AB = CK ( gt )
⇒ΔABH=ΔKCA(c−g−c)⇒ΔABH=ΔKCA(c−g−c)
⇒AH=AK⇒AH=AK ( cạnh t/ứng ) ( đpcm )
Vậy...
xét ^A =<90
tgADB vuong tai D vây goc ngoài tai đĩnh B tù =>^ABH >90
tuong tư tgAEC => ^ACK > 90
măt khác HD vgóc AC ; KE vgóc AB
vây ^ABH và ^ACK là các góc có cạnh tuong ứng vuong góc
cã hai góc đều tù do đó ^ABH=^ACK
mặt khác AB=CK ; AC=BH
nên tgABH=tgKCA(cgc) =>AH=AK
xet ^A>90 vây BD. CE nằm ngoài tgABC
lâp luân tương tư ta có AH=AK