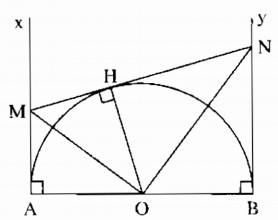
Cho nửa đường tròn đường kính AB, trên đó lấy một điểm M. Trên đường kính AB lấy một điểm C sao cho AC < BC. Trên nửa mặt phẳng bờ AB có chứa M, kẻ các tia Ax, By vuông góc với AB. Đường thẳng qua M vuông góc với MC cắt Ax tại điểm P, đường thẳng qua C vuông góc với CP cắt By tại điểm Q. Gọi D là giao điểm của CP, AM; gọi E là giao điểm của CQ; BM. Chứng minh rằng:
a) DE // AB.
b) Bốn điểm B, C, M, Q cùng nằm trên một đường tròn.