Giải hệ phương trình sau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Thay x = 3, y = 5 vào vế trái của phương trình (3) ta được:
VT = 5.3 – 2.5 = 15 – 10 = 5 = VP
Vậy (x; y) = (3; 5) là nghiệm của phương trình (3).
Hệ phương trình đã cho có nghiệm (x; ) = (3; 5)


Thay x = -3, y = 31/5 vào vế trái của phương trình (2), ta được:
VT = -3.(-3) + 2.31/5 = 9 + 62/5 = 107/5 ≠ 22 = VP
Vậy (x; y) = (-3; 31/5 ) không phải là nghiệm của phương trình (2).
Hệ phương trình đã cho vô nghiệm.

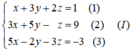
Nhân phương trình (2) với 2 rồi cộng với phương trình (1) và nhân phương trình (2) với 3 rồi trừ đi phương trình (3), phương trình (2) giữ nguyên ta được:
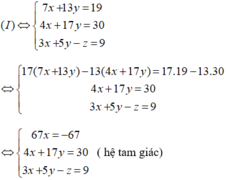
Giải hệ phương trình trên ta được x = -1; y = 2; z = -2.
Vậy hệ phương trình có nghiệm (x; y; z) = (-1; 2; -2)

\(b,ĐK:-\dfrac{1}{3}\le x\le2\\ PT\Leftrightarrow3x+1=4x^2-16x+16\\ \Leftrightarrow4x^2-19x+15=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{15}{4}\left(ktm\right)\\x=1\left(tm\right)\end{matrix}\right.\Leftrightarrow x=1\\ d,\Leftrightarrow\left\{{}\begin{matrix}x=5-3y\left(1\right)\\\left(5-3y\right)^2+2y^2=25\left(2\right)\end{matrix}\right.\\ \left(2\right)\Leftrightarrow11y^2-30y=0\\ \Leftrightarrow y\left(11y-30\right)=0\Leftrightarrow\left[{}\begin{matrix}y=0\Rightarrow x=5-3\cdot0=5\\y=\dfrac{30}{11}\Rightarrow y=5-3\cdot\dfrac{30}{11}=-\dfrac{35}{11}\end{matrix}\right.\)
Vậy \(\left(x;y\right)\in\left\{\left(5;0\right);\left(-\dfrac{35}{11};\dfrac{30}{11}\right)\right\}\)
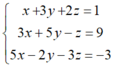
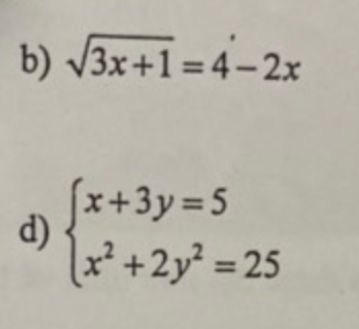


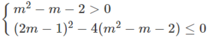
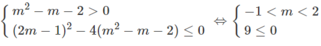
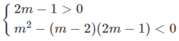
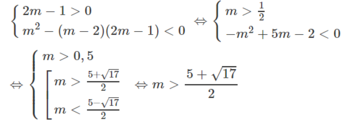
$\begin{cases}xy+x^2=1+y\\xy+y^2=1+x\end{cases}$
`=>xy+x^2-xy-y^2=1+y-1-x`
`<=>x^2-y^2=y-x`
`<=>(x-y)(x+y)+x-y=0`
`<=>(x-y)(x+y+1)=0`
`+)x=y`
`=>x^2+x^2=1+x`
`<=>2x^2-x-1=0`
`<=>x=y=1\or\x=y=-1/2`
`+)x=-y-1`
`=>y(-y-1)+(-y-1)^2=1+y`
`<=>-y^2-y+y^2+2y+1=y+1`
`<=>y+1=y+1` luôn đúng.
Vậy `(x,y) in (1,1),(-1/2,-1/2),(-y-1,y)`