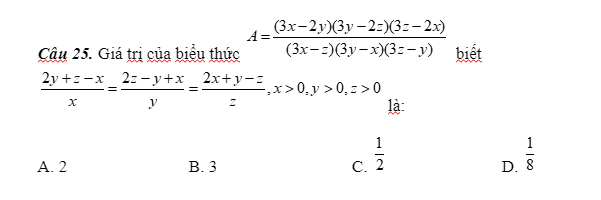Mọi người giải dùm em câu 38 với ạ 👉👈
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QL
1
29 tháng 3 2021
Câu I:
1) Ta có: \(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}+2}{\sqrt{x}}-\dfrac{x+\sqrt{x}-4}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\)
\(=\left(\dfrac{x}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{x+\sqrt{x}-4}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\dfrac{\sqrt{x}-1+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{x+x+\sqrt{x}-2-x-\sqrt{x}+4}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x+2}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}-1}{1}\)
\(=\dfrac{x+2}{\sqrt{x}}\)
2) Để P=3 thì \(\dfrac{x+2}{\sqrt{x}}=3\)
\(\Leftrightarrow x+2=3\sqrt{x}\)
\(\Leftrightarrow x-3\sqrt{x}+2=0\)
\(\Leftrightarrow x-\sqrt{x}-2\sqrt{x}+2=0\)
\(\Leftrightarrow\sqrt{x}\cdot\left(\sqrt{x}-1\right)-2\left(\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-2=0\\\sqrt{x}-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=2\\\sqrt{x}=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\left(nhận\right)\\x=1\left(loại\right)\end{matrix}\right.\)
Vậy: Để P=3 thì x=4
DT
7 tháng 1 2022
III,
1. different
2. between
3. out
4. well
5. downstairs
6. written
7. has lived
8. as cold as
9. to study
10. taking
11. have to
12. between
13. himself
14. How long
15. on
IV,
1. My family used to visit Sa Pa last summer vacation.
2. They used to go to school by bus last year.
3. Na isn’t as beautiful as Trang.
4. French is more difficult than English.
5. They have lived here for 10 years.
6. She enjoys swimming and outdoor activities.
1N
giúp mình(em) với ạ =((
1
1 tháng 7 2023
a: =(-3/2)*(-2/3)+(5/2-3/4):7/4
=1+7/4:7/4=1+1=2
b: \(=\dfrac{1}{3}\left(\dfrac{3}{1\cdot4}+\dfrac{3}{4\cdot7}+...+\dfrac{3}{100\cdot103}\right)\)
\(=\dfrac{1}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{100}-\dfrac{1}{103}\right)\)
=1/3*102/103=34/103
HP
16 tháng 8 2021
ĐK: \(x\ne\dfrac{\pi}{4}+k\pi;x\ne\dfrac{\pi}{2}+k2\pi\)
\(tan2x.tanx=1\)
\(\Leftrightarrow\dfrac{sin2x.sinx}{cos2x.cosx}=1\)
\(\Leftrightarrow sin2x.sinx=cos2x.cosx\)
\(\Leftrightarrow\dfrac{1}{2}\left(cosx-cos3x\right)=\dfrac{1}{2}\left(cos3x+cosx\right)\)
\(\Leftrightarrow cos3x=0\)
\(\Leftrightarrow3x=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{k\pi}{3}\)
20 tháng 1 2022
a: Xét ΔMEB vuông tại M và ΔACB vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔMEB\(\sim\)ΔACB
Xét ΔDMC vuông tại M và ΔABC vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔDMC\(\sim\)ΔABC
b: BC=30cm
4 tháng 12 2021
Áp dụng tc dtsbn:
\(\dfrac{2y+z-x}{x}=\dfrac{2z-y+x}{y}=\dfrac{2x+y-z}{z}=\dfrac{2x+2y+2z}{x+y+z}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2\\ \Rightarrow\left\{{}\begin{matrix}2y+z-x=2x\\2z-y+x=2y\\2x+y-z=2z\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2y+z=3x\\2z+x=3y\\2x+y=3z\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3x-2y=z\\3y-2z=x\\3z-2x=y\end{matrix}\right.;\left\{{}\begin{matrix}3x-z=2y\\3y-x=2z\\3z-y=2z\end{matrix}\right.\\ \Rightarrow P=\dfrac{xyz}{2x\cdot2y\cdot2z}=\dfrac{1}{8}\)
Chọn D
20 tháng 1 2022
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\)
Do đó: ΔHBA\(\sim\)ΔHAC
Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{C}\) chung
DO đó: ΔABC\(\sim\)ΔHAC
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\)
