GIÚP EM VỚI Ạ Cho hình chóp S.ABC có đây là tam giác ABC với AB=4a, đường cao CH =a (H thuộc AB) và góc ACH = 45° Hai mặt bên (SAB),(SAC) cũng vuông góc với đáy, SA=5a a) Chứng minh SA vuông góc với mặt phẳng (ABC). b) Chứng minh (SCH) vuông góc với (SAB). c) Trên các đường thẳng vuông góc với mặt phẳng (ABC) kẻ từ B,C, lấy lần lượt các điểm B',C' nằm cùng phía S so với (ABC) sao cho BB'=3a,CC' =a. Tính góc giữa hai mặt phẳng (SB'C'), (ABC).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AB\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow BC\perp\left(SAB\right)\)
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\\BH\in\left(ABC\right)\end{matrix}\right.\) \(\Rightarrow SA\perp BH\)
Lại có \(BH\perp AC\) (do BH là đường cao)
\(\Rightarrow BH\perp\left(SAC\right)\)
Mà \(SC\in\left(SAC\right)\)
\(\Rightarrow BH\perp SC\)

Do (SAB) và (SAC) vuông góc với đáy (ABC)
Và (ABC) ∩ (SAC) = SA nên SA ⊥ (ABC)
BC ⊥ AH, BC ⊥ SA
⇒ BC ⊥ ((SAH)
Mà BC ⊂ (SBC) nên (SAH) ⊥ (SBC)

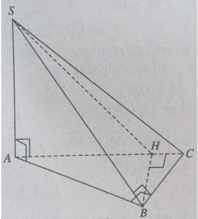
a) BC ⊥ SA & BC ⊥ AB) ⇒ BC ⊥ (SAB)
⇒ BC ⊥ SB.
⇒ tam giác SBC vuông tại B.
b) BH ⊥ AC & BH ⊥ SA ⇒ BC ⊥ (SAC)
⇒ (SBH) ⊥ (SAC).
c) d[B, (SAC)] = BH. Ta có:
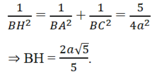


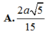
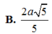
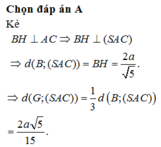
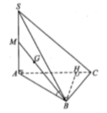
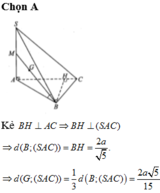
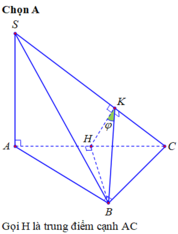

a: (SAB) và (SAC) cùng vuông góc (ABC)
(SAB) cắt (SAC)=SA
=>SA vuông góc (ABC)
b: SA vuông góc CH
CH vuông góc AB
=>CH vuông góc (SAB)
=>(SCH) vuông góc (SAB)