Cho 7,2 gam hỗn hợp X gồm S và Fe vào một bình kín không có oxi. Nung bình cho đến khi phản ứng xảy ra hoàn toàn, thu được chất rắn A. Cho A tác dụng với dung dịch H2SO4loãng, dư thu được 2,24 lít hỗn hợp khí Y (đktc). Tỉ khối của Y so với H2 là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 3 2019
Đáp án C
Nung M: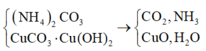 
Chất rắn X lại phản ứng với HNO3 tạo NO2 nên X có Cu
Khí Y phản ứng với HC1 tạo muối nên Y có NH3
Mà ta thấy ở nhiệt độ cao thì 3CuO + 2NH3 3CuO + N2 + 3H2O
Do phản ứng xảy ra hoàn toàn nên NH3 dư, X chỉ có Cu. n NO 2 = 0 , 6
2 tháng 11 2019
Đáp án A
Bài này có thể giải theo kinh nghiệm,
hoặc biện luận rào số mol hỗn hợp A.
Từ đó ⇒ giới hạn của chất rắn C
Trường hợp xả ra đó là:
Fe pứ hết và Cu chỉ pứ 1 phần
⇒ C gồm Ag và Cu chưa tan.
+ Sơ đồ ta có:
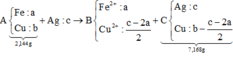
PT theo khối lượng oxit:
40c = 2,56 Û c = 0,064 mol
⇒ CM AgNO3 = 0,064 ÷ 0,2 = 0,32
20 tháng 5 2019
Bài này có thể giải theo kinh nghiệm, hoặc biện luận rào số mol hỗn hợp A.
Từ đó ⇒ giới hạn của chất rắn C
Trường hợp xả ra đó là:
Fe pứ hết và Cu chỉ pứ 1 phần ⇒ C gồm Ag và Cu chưa tan.
+ Sơ đồ ta có:
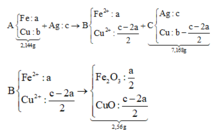
PT theo khối lượng oxit: 40c = 2,56 Û c = 0,064 mol
⇒ CM AgNO3 = 0,064 ÷ 0,2 = 0,32
Đáp án A
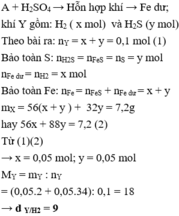
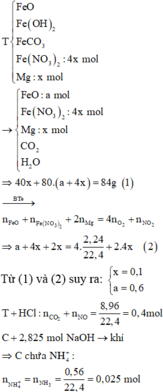
A + H2SO4 → Hỗn hợp khí ⇒ Fe dư; khí Y gồm: H2 ( x mol) và H2S (y mol)
⇒ x + y = 0,1 mol (1)
Bảo toàn S: nH2S = nFeS = nS = y mol
nFe dư = nH2 = x
Bảo toàn Fe: nFe = nFeS + nFe dư = x + y
mX = 56(x + y ) + 32y = 7,2g (2)
Từ (1)(2) ⇒ x = 0,05 mol; y = 0,05 mol
MY = mY : nY = (0,05.2 + 0,05.34) : 0,1 = 18 ⇒ dY/H2 = 9
Gọi \(\left\{{}\begin{matrix}n_{Fe}=a\left(mol\right)\\n_{FeS}=b\left(mol\right)\end{matrix}\right.\left(đk:a,b>0\right)\)
TH1: S dư
Vậy toàn bộ lượng khí sinh ra là H2S
\(d_{Y\text{/}H_2}=d_{H_2S\text{/}H_2}=\dfrac{34}{2}=17\)
TH2: Fe dư
\(n_{khí}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\)
Bảo toàn KL: \(m_A=m_X=7,2\left(g\right)\)
PTHH:
\(Fe+2HCl\rightarrow FeCl_2+H_2\uparrow\)
a----------------------------->a
\(FeS+2HCl\rightarrow FeCl_2+H_2S\uparrow\)
b-------------------------------->b
Ta có hệ phương trình: \(\left\{{}\begin{matrix}56a+88b=7,2\\a+b=0,1\end{matrix}\right.\)
\(\Leftrightarrow a=b=0,05\left(TM\right)\)
\(M_Y=\dfrac{0,05.\left(2+34\right)}{0,1}=18\left(g\text{/}mol\right)\\ \rightarrow d_{Y\text{/}H_2}=\dfrac{18}{2}=9\)