Cho tam giác ABC . Hai đường cao BM và CN cắt nhau tại H.
a. Chứng minh rằng AH vuông góc BC.
b. Khi góc BAC = 70 độ . Hãy tính góc BHNvà góc MHN.
c. Khi góc ACB = 50 độ . Hãy tính góc AHM.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 9 2023
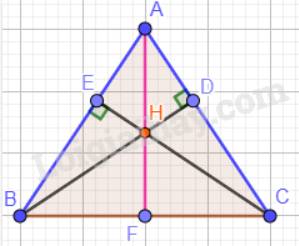
a) Tam giác ABC cân tại A nên: \(\widehat {ABC} = \widehat {ACB} = 70^\circ \).
Tổng ba góc trong một tam giác bằng 180° nên: \(\widehat {BAC} = 180^\circ - 70^\circ - 70^\circ = 40^\circ \).
b) Xét tam giác vuông ADB và tam giác vuông AEC có:
AB = AC (tam giác ABC cân);
\(\widehat A\) chung.
Vậy \(\Delta ADB = \Delta AEC\)(cạnh huyền – góc nhọn). Suy ra: BD = CE ( 2 cạnh tương ứng).
c) Trong tam giác ABC có H là giao điểm của hai đường cao BD và CE nên H là trực tâm trong tam giác ABC hay AF vuông góc với BC.
Xét hai tam giác vuông AFB và AFC có:
AB = AC (tam giác ABC cân);
AF chung.
Vậy \(\Delta AFB = \Delta AFC\)(cạnh huyền – cạnh góc vuông). Suy ra: \(\widehat {FAB} = \widehat {FAC}\) ( 2 góc tương ứng) hay \(\widehat {BAH} = \widehat {CAH}\).
Vậy tia AH là tia phân giác của góc BAC.
11 tháng 5 2022
a: Xét ΔCKB có
KF là đường cao
BA là đường cao
KF cắt BA tại E
DO đó: CE⊥BK
b: \(\widehat{AEF}=180^0-50^0=130^0\)
6 tháng 3 2022
a: ta có: ΔABC cân tại A
mà AH là đường phân giác
nên AH vừa là đường cao vừa là đừog trung tuyến
b: Vì H là trung điểm của BC
nên BH=CH=4cm
\(AH=\sqrt{AB^2-AH^2}=2\sqrt{21}\left(cm\right)\)
c: Xét ΔBIC có
IH là đường cao
IH là đường trung tuyến
Do đó:ΔBIC cân tại I
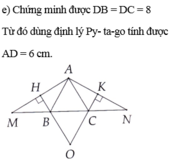
a: XétΔABC có
BM là đường cao
CN là đường cao
BM cắt CN tại H
Do đó: H là trực tâm của ΔABC
Suy ra: AH vuông góc với BC
b: \(\widehat{MHN}=360^0-90^0-90^0-70^0=110^0\)
=>\(\widehat{BHN}=70^0\)