Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ai trả lời giúp mk đi , cả lời giải và phép tính mai mk fai nộp rồi
ai giỏi thì giúp mình với mình cảm ơn rất nhiều !!!!!
Nhanh lên nhé mai mình phải nộp rồi
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
a: Xét ΔABD và ΔACE có
AB/AC=AD/AE
góc A chung
Do đó: ΔABD\(\sim\)ΔACE
b: ta có: ΔABD\(\sim\)ΔACE
nên \(\dfrac{S_{ABD}}{S_{ACE}}=\left(\dfrac{AB}{AC}\right)^2=\left(\dfrac{5}{7}\right)^2=\dfrac{25}{49}\)
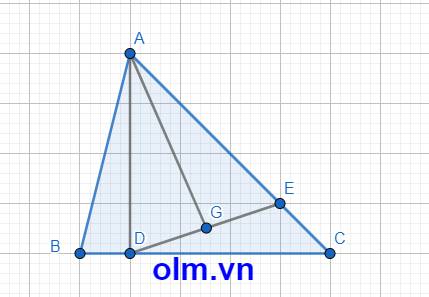
SADE = 2\(\times\)SAGE ( vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy DE và DE = 2\(\times\) GE )
⇒ SADE = 36 \(\times\) 2 = 72 (cm2)
SADE = \(\dfrac{3}{4}\)\(\times\)SADC (vì hai tam giác có chung chiều cao hạ từ Đỉnh D xuống đáy AC và AE = \(\dfrac{3}{4}\)AC)
⇒ SACD = 72 : \(\dfrac{3}{4}\) = 96 (cm2)
DC = BC - BD = BC - \(\dfrac{1}{5}\)BC = \(\dfrac{4}{5}\)BC
SADC = \(\dfrac{4}{5}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và DC = \(\dfrac{4}{5}\)BC)
⇒ SABC = 96 : \(\dfrac{4}{5}\) = 120 (cm2)
Tỉ số phần trăm diện tích tam giác ADE và diện tích tam giác ABC là:
72 : 120 = 0,6
0,6 = 60%
Đáp số: 60%
