Chọn C

PTHH: Al2O3+6HCl➝2AlCl3+3H2O(1)

a)nAl2O3=\(\dfrac{10,2}{102}\)=0,1(mol)

   mHCl=\(\dfrac{5\%.219}{100\%}\)=10,95(g)

   ⇒nHCl=\(\dfrac{10,95}{36,5}\)=0,3(mol)

Xét tỉ lệ Al2O3:\(\dfrac{0,1}{1}\)=0,1

Xét tỉ lệ HCl:\(\dfrac{0,3}{6}\)=0,05

⇒HCl pứng hết,Al2O3 còn dư

Theo PTHH(1) ta có nAl2O3 pứng=\(\dfrac{nHCl}{6}\)=\(\dfrac{0,3}{6}\)=0,05(mol)

⇒nAl2O3 dư=nAl2O3ban đầu-nAl2O3 pứng=0,1-0,05=0,05(mol)

⇒mAl2O3 dư=0,05.102=5,1(g)

b) C%HCl=\(\dfrac{0,3.36,5}{219+10,2}\).100%=4,8%

     nAlCl3=0,1(mol)

⇒C%AlCl3=\(\dfrac{0,1.136,5}{10,2+219}\).100%=6%

lx

Lx

B

C

A

B

C

D

2:

a: =2xy^4+12xy^4+x^2=14xy^4+x^2

b: 3a^2b^3+ab-8a^2b^3-2ab

=ab-2ab+3a^2b^3-8a^2b^3

=-5a^2b^3-ab

3:

a: BC=căn 3^2+4^2=5cm

b: Xét ΔABD vuông tại A và ΔABC vuông tại A có

AB chung

AD=AC

=>ΔABD=ΔABC

c: Xét ΔBEA vuông tại E và ΔBFA vuông tại F có

BA chung

góc EBA=góc FBA

=>ΔBEA=ΔBFA

=>EA=FA

=>ΔAEF cân tại A

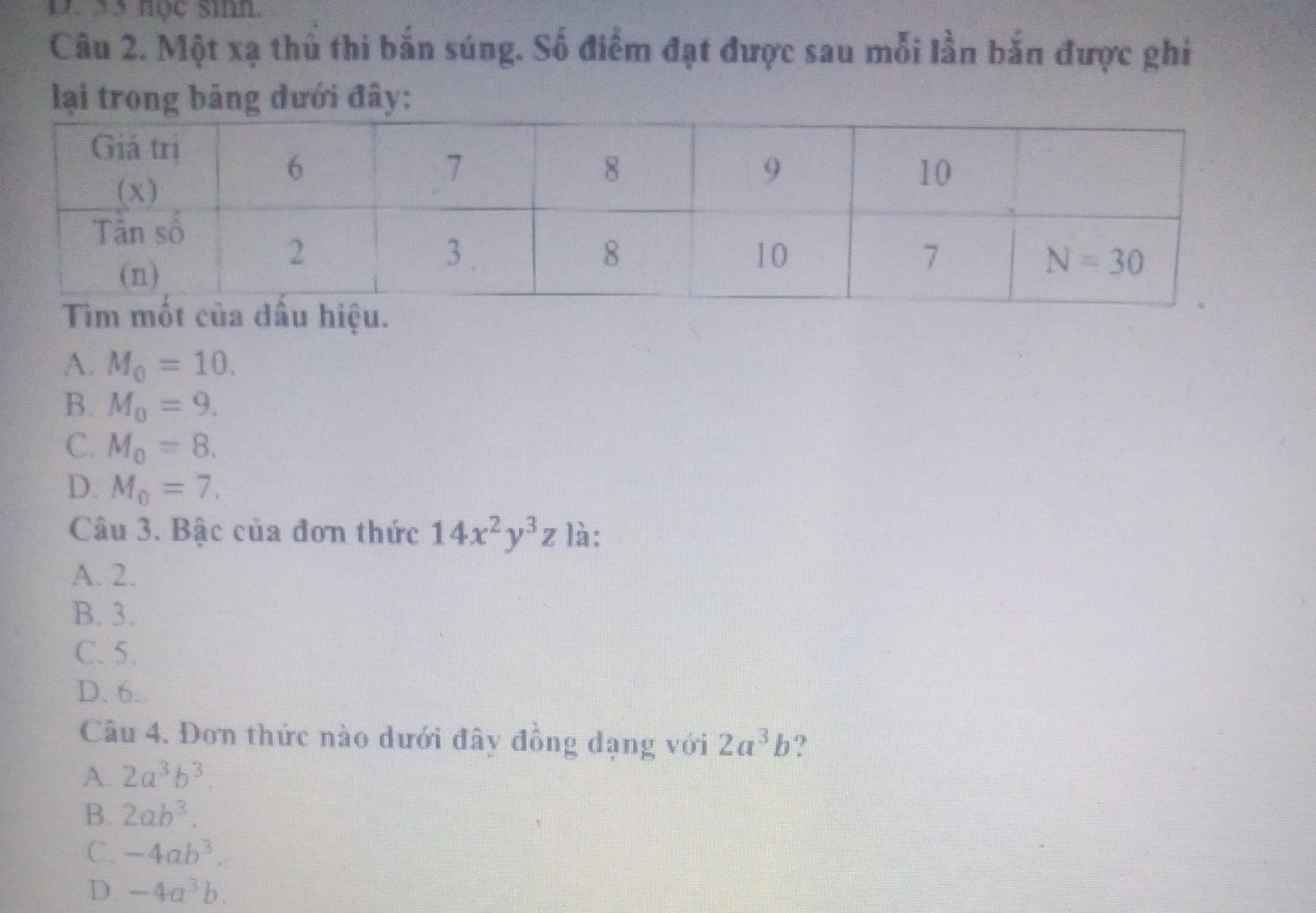
Bài 4 :                              

                              \(n_{H2}=\dfrac{V_{H2}}{22,4}=\dfrac{3,36}{22,4}=0,15\left(mol\right)\)

Pt :                         \(2Al+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2|\)

                                 2           3                     1              3

                               0,1        0,15                 0,05        0,15

  a)                            \(n_{Al}=\dfrac{0,15.2}{3}=0,1\left(mol\right)\)

                                       ⇒ \(m_{Al}=n_{Al}.M_{Al}\)

                                                   = 0,1 . 27

                                                   = 2,7 (g)

                                      \(m_{Cu}=10-2,7=7,3\left(g\right)\)

                              ⁰/₀Al = \(\dfrac{m_{Al}.100}{m_{hh}}=\dfrac{2,7.100}{10}=27\)⁰/₀

                            ⁰/₀Cu = \(\dfrac{m_{Cu}.100}{m_{hh}}=\dfrac{7,3.100}{10}=13\)⁰/₀

b)                           \(n_{Al2\left(SO4\right)3}=\dfrac{0,15.1}{3}=0,05\left(mol\right)\)

                             ⇒ \(m_{Al2\left(SO4\right)3}=n_{Al2\left(SO4\right)3.}M_{Al2\left(SO4\right)3}\)

                                                  = 0,05 . 342

                                                   = 17,1 (g)

                                     \(n_{H2SO4}=\dfrac{0,1.3}{2}=0,15\left(mol\right)\)

                                      ⇒ \(m_{H2SO4}=n_{H2SO4}.M_{H2SO4}\)

                                                        = 0,15 .98

                                                        = 14,7 (g)

              \(C_{H2SO4}=\dfrac{m_{ct}.100}{m_{dd}}\Rightarrow m_{dd}=\dfrac{m_{ct}.100}{C}=\)\(\dfrac{14,7.100}{15}=98\left(g\right)\)

                m_{dung dịch sau phản ứng} = (m_Al + m_Cu) + m_H2SO4 - m_H2

                                                    = 10 + 98 - (0,15 . 2)

                                                     =107,7 (g)

                       \(C_{Al2\left(SO4\right)3}=\dfrac{m_{ct}.100}{m_{dd}}=\dfrac{17,1.100}{107,7}=15,88\)⁰/₀

 Chúc bạn học tốt

Mình xin lỗi bạn nhé , bạn sửa kết quả : phần trăm của của đồng '13⁰/₀' thành ' 73⁰/₀' giúp mình 

Gọi \(M\left(x;y\right)\) là điểm biểu diễn z trên mặt phẳng tọa độ

Gọi \(A\left(-2;1\right)\) ; \(B\left(2;3\right)\) ; \(C\left(-1;2\right)\)

\(\Rightarrow\overrightarrow{AB}=\left(4;2\right)\Rightarrow AB=2\sqrt{5}\)

Từ \(\left|z+2-i\right|+\left|z-2-3i\right|=2\sqrt{5}\Leftrightarrow MA+MB=2\sqrt{5}\)

\(\Leftrightarrow MA+MB=AB\Leftrightarrow\) M nằm trên đoạn thẳng AB

\(\left|z+i-2i\right|=MC\) đạt GTNN khi và chỉ khi M là hình chiếu vuông góc của C lên AB

Phương trình đường thẳng AB:

\(1\left(x+2\right)-2\left(y-1\right)=0\Leftrightarrow x-2y+4=0\)

Phương trình đường thẳng d qua C và vuông góc AB:

\(2\left(x+1\right)+1\left(y-2\right)=0\Leftrightarrow2x+y=0\)

Tọa độ M là nghiệm: \(\left\{{}\begin{matrix}x-2y+4=0\\2x+y=0\end{matrix}\right.\) \(\Rightarrow M\left(-\dfrac{4}{5};\dfrac{8}{5}\right)\)

\(\Rightarrow\overrightarrow{MC}=\left(-\dfrac{1}{5};-\dfrac{2}{5}\right)\Rightarrow MC=\dfrac{\sqrt{5}}{5}\)

Đáp án B