Cho tam giác ABC vuông tại A có AB = 6 cm, BC = 10 cm . Quay một vòng quanh cạnh AB cố định ta được một hình nón có diện tích xung quanh là??
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Tam giác ABC vuông tại A có:
sin A B C ⏜ = A C B C ⇒ A C = sin 30 ∘ .2 a = a c os A B C ⏜ = A C B C ⇒ A B = c os 30 ∘ .2 a = a 3 .
Quay Δ A B C quanh trục AB ta được hình nón có bán kính đáy r = A C = a .
=> Diện tích xung quanh hình nón trên là S 1 = π r l = π . a .2 a = 2 π a 2 . Và diện tích mặt cầu đường kính AB là: S 2 = 4 π R 2 = 4 π a 3 2 2 = 3 π a 2 ⇒ S 1 S 2 = 2 π a 2 3 π a 2 = 2 3 .

Hướng dẫn làm bài:
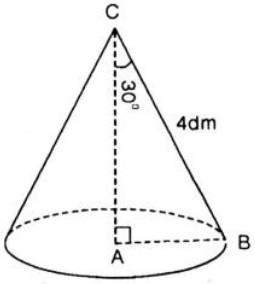
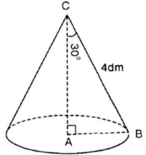
Trong tam giác vuông ABC, ta có:
AB=BC.sinC=BC.sin300=4.1/2=2(dm)
AC=BC.cosC=BC.cos300=4.√3/2=2√3(dm)
Ta có: Sxq = πRl = π. 2. 4 = 8 π (dm2)
V=1/3 π R2 h=1/3 π.22.2√3=8√3.π/3(dm3)

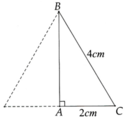
a, Dễ dàng tính được
AC = 2cm, AB = 2 3 cm và S h n = πAC . BC = 8 π
=> V h n = 1 3 πAC 2 . AB = 8 3 3 π
b, Tính được S t p = 12 πcm 2
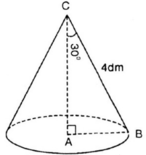
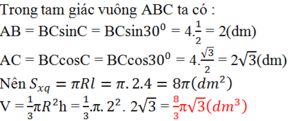
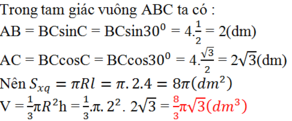
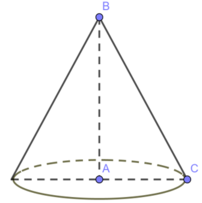

Quay tam giác \(ABC\) quanh cạnh \(AB\) cố định thu được hình nón có đỉnh là \(B\) đáy là đường tròn đáy bán kính \(AC\).
Theo định lí Pythagore ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC=\sqrt{10^2-6^2}=8\left(cm\right)\)
Diện tích xung quanh hình nón là :
\(S_{xq}=\pi rl=\pi.AC.BC=80\pi\left(cm^2\right)\)