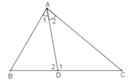
Trong ΔABD ta có ∠D1 là góc ngoài tại đỉnh D

∠D1 = ̂B + ∠A1 (tính chất góc ngoài của tam giác)

Trong ΔADC ta có ∠D2 là góc ngoài tại đỉnh D

∠D2 = ̂C + ∠A2 (tính chất góc ngoài của tam giác)

Ta có: ∠B > ∠C (gt); ∠A1 = ∠A2 (gt)

⇒∠D1 - ∠D2 = (B + ∠A1) - (C + ∠A2) = ∠B - ∠C = 20o

Lại có: ∠D1 + ∠D2 = 180o (hai góc kề bù)

⇒∠D1 = (180o + 20o):2 = 100o

⇒∠D1 = (100o - 20o) = 80o

Đặt \(\widehat{ADC}=b;\widehat{ADB}=a\)

Ta có: \(a+\widehat{B}+\widehat{BAD}=b+\widehat{C}+\widehat{CAD}\)

\(\Leftrightarrow a+\widehat{C}+20^0=b+\widehat{C}\)

\(\Leftrightarrow a-b=-20\)

mà a+b=180

nên 2a=160

=>a=80

=>b=100

Ta có:B-C=20

Ta lại có: BAD=DAC( tính chất tia phân giác).

Do:ADC=BAD+ABD( tính chất góc ngoài)

ADB=DAC+ACD( tính chất góc ngoài)

→ADC-ADB= B-C=20→ADC=ADB+20 (1).

Lại do ADC+ADB=180 (2)

Thay (1) vào (2) ta được:

20+ADB+ADB=180

→ 20+2ADB= 180

→ 2ADB=160

→ ADB=80 (3)

Thay (3) vào (1) ta được:

ADC=80+20

→ ADC=100

Vì ADB là goc là góc ngoài của ∆ADC

Suy ra góc ADB =góc DAC+C mà AD là phân giác góc A

Suy ra ADB=C+A/2 (1)

Vì ADC là góc ngoài của_∆ADB

Suy ra ADC=BAD+

Mà Ad là phân giác cẩu

Suy ra ADC=B+A/2 (2)

Từ 1 và 2 suy ra B-C =ADC-ADB=20

Mà ADC+ ADB =180(kề bù)

Suy ra ADC=(180+20)/2=100

Suy ra ADB=180-100=80

Vậy ADB =80

Vậy ADC=100

Xét tam giác ABC: \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\Rightarrow\widehat{B}+\widehat{C}=180^0-\widehat{A}\)

Mặt khác: \(\widehat{B}-\widehat{C}=18^0\Rightarrow\left\{{}\begin{matrix}\widehat{B}=\dfrac{180^0-\widehat{A}+18^0}{2}=99^0-\dfrac{\widehat{A}}{2}\\\widehat{C}=99^0+\dfrac{\widehat{A}}{2}-18^0=81^0-\dfrac{\widehat{A}}{2}\end{matrix}\right.\)

Xét tam giác ABD: \(\widehat{ADC}=\widehat{BAD}+\widehat{B}=\dfrac{\widehat{A}}{2}+99^0-\dfrac{\widehat{A}}{2}=99^0\)

\(\widehat{ABD}=180^0-\widehat{ADC}=81^0\)

ta có