Tập hợp tất cả các giá trị thực của tham số m để phương trình x6 +6x4 -m3x3 +(15 -3m2)x2 -6mx +10 =0 có đúng hai nghiệm phân biệt thuộc đoạn \(\left[\dfrac{1}{2};2\right]\) là?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn đáp án B
Phương trình đã cho tương đương với:
![]()
![]()
![]()
Xét hàm số f t = t 3 + 3 t trên ℝ
Tacó f ' t = 3 t 2 + 3 > 0 , ∀ t ∈ ℝ nên hàm số f t đồng biến trên ℝ
Suy ra
![]()
![]()
Xét hàm số g x = x + 1 x trên 1 2 ; 2
Ta có g ' x = 1 - 1 x 2
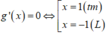
Bảng biến thiên:
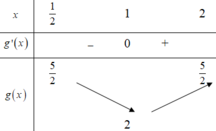
Dựa vào bảng biến thiên, để phương trình đã cho có hai nghiệm phân biệt trên 1 2 ; 2
⇔ Đường thẳng y = m cắt đồ thị hàm số g x = x + 1 x tại hai điểm phân biệt trên 1 2 ; 2
⇔ 2 < m ≤ 5 2

Bất phương trình tương đương với:
![]()
![]()
![]()
![]()
![]()
![]()
trong đó hàm số f ( t ) = t 3 + 3 t đồng biến trên R.
Vậy ![]()
![]()
Có 5 số nguyên thoả mãn.
Chọn đáp án D.

Xét phương trình hoành độ giao điểm\(x^2\)+4x-m=0 <=> x^2+4x=m, đây là kết hợp của 2 hàm số (P):y=\(x^2\)+4x và (d):y=m.
Khi vẽ đồ thị ta thấy parabol đồng biến trên khoảng (-2;+∞)=> Điểm giao giữa parabol và đồ thị y=m là điểm duy nhất thỏa mãn phương trình có duy nhất 1 nghiệm thuộc khoảng (-3;1).Vậy để phương trình có 1 nghiệm duy nhất <=> delta=0 <=>16+4m=0<=>m=-4.
mình trình bày hơi dài mong bạn thông cảm 

- Đặt \(a=x^2-2x\left(a\ge-1\right)\)
PTTT \(3\sqrt{a+3}=a+m\left(a\ge-m\right)\)
\(\Leftrightarrow9\left(a+3\right)=\left(a+m\right)^2=a^2+2am+m^2=9a+27\)
\(\Leftrightarrow a^2+a\left(2m-9\right)+m^2-27=0\)
Có : \(\Delta=\left(2m-9\right)^2-4\left(m^2-27\right)=4m^2-36m+81-4m^2+108\)
\(=-36m+189\)
- Để phương trình đề có 2 nghiệm phân biệt :
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\\left(a_1+1\right)\left(a_2+1\right)>0\\a_1+1+a_2+1>0\end{matrix}\right.\)
Lại có : Theo vi ét : \(\left\{{}\begin{matrix}a_1+a_2=-2m+9\\a_1a_2=m^2-27\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\Delta>0\\a_1a_2+a_1+a_2+1>0\\a_1+a_2+2>0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-36m+189>0\\m^2-27-2m+9+1=m^2-2m-17>0\\-2m+9+2=-2m+11>0\end{matrix}\right.\)
\(\Rightarrow m=\left(-\infty;1-3\sqrt{2}\right)\cup\left(1+3\sqrt{2};\dfrac{21}{4}\right)\) ( * )
- Có : \(x^2-2x=a\)
- Đặt \(f\left(x\right)=x^2-2x\)
- Ta có đồ thị \(x^2-2x=0\)
- Từ độ thị hàm số : Để phương trình \(x^2-2x=a\) có 2 nghiệm phân biệt trong đoạn 0, 3 thì \(a=(-1;0]\)
Lại có : \(a=[-m;+\infty)\)
\(\Rightarrow-m\le0\)
\(\Rightarrow m\ge0\)
- Kết hợp với ( * )
\(\Rightarrow m\in\left(1+3\sqrt{2};\dfrac{21}{4}\right)\)
Vậy ...

Chọn đáp án D.
Bất phương trình tương đương với
![]()
![]()
![]()
![]()
![]()
trong đó hàm số f t = t 3 + 3 t đồng biến trên R
Vậy y c b t ⇔ x 2 - m x + 1 ≥ 0 , ∀ x
![]()
Có 5 số nguyên thoả mãn

Đáp án B
P T ⇔ x − m x 2 + x m + m 2 − 3 x − m x + m = 0
⇔ x − m x 2 + m x − 3 x + m 2 − 3 m = 0 ⇔ x = m g x = x 2 + m − 3 x + m 2 − 3 m
PT có 3 nghiệm phân biệt ⇔ g x = 0 có 2 nghiệm phân biệt khác m
⇔ Δ = m − 3 2 − 4 m 2 − 3 m > 0 g m = 3 m 2 − 6 m ≠ 0 ⇔ − 3 m 2 + 6 m + 9 > 0 m ≠ 0 ; m ≠ 6 ⇔ − 1 < m < 3 m ≠ 0 ; m ≠ 2

