Cho hình chữ nhật ABCD có AB=2 AC, M là trung điểm của AB. Lấy điểm H trên AB sao cho góc ADH=15 độ. Gọi K là giao điểm của DM và CH. Chứng minh DH=DK
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


LỜI GIẢI :
Trên nửa mặt phẳng chứa C bờ là đường thẳng DH dựng tam giác đều DHN .Gọi Q là trung điểmDC ta có :
AD = DQ = QC
DH = HN ( DHN đều )
Từ đó suy ra
Tức là CHD cân tại C .Mà (1)
Do tam giác ADM vuông cân tại A nên (2)
Xét tam giác DHK từ (1) và (2) suy ra (3)
Từ (1) và(3) suy ra tam giác DHK cân tại D Tức là DH = DK

GIẢI :
Trên nửa mặt phẳng chứa C bờ là đường thẳng DH dựng tam giác đều DHN .Gọi Q là trung điểmDC ta có :
AD = DQ = QC
DH = HN ( DHN đều )
Từ đó suy ra
Tức là CHD cân tại C .Mà (1)
Do tam giác ADM vuông cân tại A nên (2)
Xét tam giác DHK từ (1) và (2) suy ra (3)
Từ (1) và(3) suy ra tam giác DHK cân tại D Tức là DH = DK

H thuộc AB thì góc ADH < 90o , không thể = 150o được. Bạn xem lại đề nhé

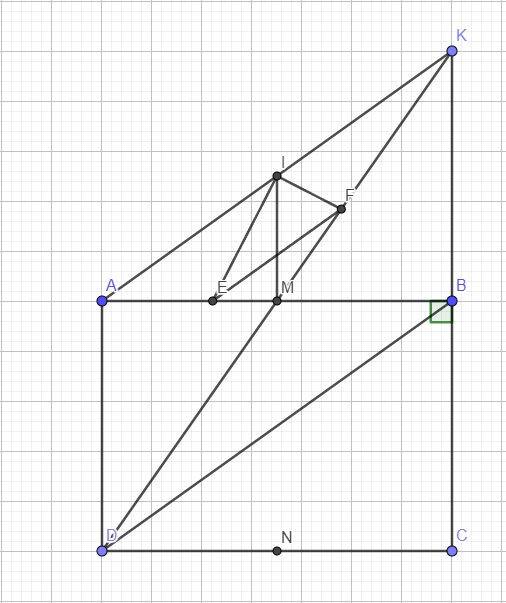
a: Xét tứ giác ADBK có
M là trung điểm chung của AB và DK
=>ADBK là hình bình hành
=>AK=DB
mà DB=AC(ABCD là hình chữ nhật)
nên AK=AC
=>ΔAKC cân tại A
b: Xét ΔIAM có IE là phân giác
nên \(\dfrac{ME}{EA}=\dfrac{IM}{IA}\)
mà IA=IK
nên \(\dfrac{ME}{EA}=\dfrac{IM}{IK}\)
Xét ΔIMK có IF là phân giác
nên \(\dfrac{IM}{IK}=\dfrac{MF}{FK}\)
=>\(\dfrac{ME}{EA}=\dfrac{MF}{FK}\)
Xét ΔMAK có \(\dfrac{ME}{EA}=\dfrac{MF}{FK}\)
nên EF//AK
Ta có: EF//AK
AK//BD(AKBD là hình bình hành)
Do đó: EF//BD

a.
Xét tứ giác ADBK có: hai đường chéo AB và DK cắt nhau tại trung điểm M của mỗi đường
\(\Rightarrow ADBK\) là hình bình hành
Do ABCD là hình chữ nhật \(\Rightarrow AB\perp BC\Rightarrow AB\) là đường cao tam giác ACK
Theo cmt, ADBK là hbh \(\Rightarrow BK=AD\)
Mà \(AD=BC\) (ABCD là hcn)
\(\Rightarrow BK=BC\Rightarrow AB\) là trung tuyến tam giác ACK
\(\Rightarrow AB\) vừa là đường cao vừa là trung tuyến nên tam giác ACK cân tại A
b.
Do IE là phân giác, áp dụng định lý phân giác trong tam giác IAM:
\(\dfrac{EM}{EA}=\dfrac{IM}{IA}\) (1)
Do IF là phân giác, áp dụng định lý phân giác trong tam giác IMK:
\(\dfrac{FM}{FK}=\dfrac{IM}{IK}\) (2)
Mà I là trung điểm AK \(\Rightarrow IA=IK\) (3)
(1);(2);(3) \(\Rightarrow\dfrac{EM}{EA}=\dfrac{FM}{FK}\Rightarrow EF||AK\) (định lý Talet đảo)
Theo c/m câu a do ADBK là hình bình hành \(\Rightarrow AK||BD\)
\(\Rightarrow EF||BD\)
xin lỗi nha
em ko bit
Zậy có 2 bik ko