f(a+b)=f(ab) suy ra: là hàm hầng.

suy ra; f94)=f(2016)=5

Với mọi x thỏa mãn: f( a + b ) = f (ab) 

=>f( 0 ) = f( -1/2 . 0 ) = f ( -1/2 + 0 ) = f( -1/2 ) = -1/2 

=> f ( 2006 ) = f ( 2006 + 0 ) = f(2006 . 0 ) = f(0 ) = -1/2

Vì f(a+b)=f(ab) với mọi a, b nên ta có: f(x)=f(x+0)=f(x.0)=f(0) với mọi x\(\Rightarrow\)f(x) là hàm hằng.

Mà f(4)=5 nên f(2016)=5

Chọn C.

Đặt   t = f ( x ) → d t = f ' x d x . Đổi cận:  x = 2016 → t = f ( 2016 ) = a x = 2017 → t = f ( 2017 ) = b

Khi đó 

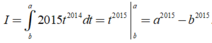
\(f\left(x\right)=\left|x-2015\right|+\left|x+2016\right|\)

a) Ta có: \(\left|x\right|=\orbr{\begin{cases}x=\frac{1}{2}\\x=-\frac{1}{2}\end{cases}}\)

+) Với \(x=\frac{1}{2}\): 

\(f\left(\frac{1}{2}\right)=\left|\frac{1}{2}-2015\right|+\left|\frac{1}{2}+2016\right|=2\)

+) Với \(x=-\frac{1}{2}\)

\(f\left(-\frac{1}{2}\right)=\left|-\frac{1}{2}-2015\right|+\left|-\frac{1}{2}+2016\right|=0\)

c) Áp dụng BĐT |x| + |y| \(\ge\)|x + y|, ta được:

\(f\left(x\right)=\left|x-2015\right|+\left|x+2016\right|=\left|2015-x\right|+\left|x+2016\right|\)

\(\ge\left|\left(2015-x\right)+\left(x+2016\right)\right|=\left|4031\right|=4031\)

(Dấu "="\(\Leftrightarrow\left(2015-x\right)\left(x+2016\right)\ge0\)

TH1: \(\hept{\begin{cases}2015-x\ge0\\x+2016\ge0\end{cases}}\Leftrightarrow-2016\le x\le2015\)

TH2: \(\hept{\begin{cases}2015-x\le0\\x+2016\le0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge2015\\x\le-2016\end{cases}}\left(L\right)\))

Vậy \(f\left(x\right)_{min}=4031\Leftrightarrow-2016\le x\le2015\)