cạch góc cạch

Ta có hình vẽ:Xét tam giác ABC và tam giác ADE có

-góc A: góc chung

-AB = AD (GT)

-BE = DC (GT)

Vậy \(\Delta\)ABC = \(\Delta\)ADE (c.g.c)

Ta có:

AB=AD

BE=DC

=>AE=AC

Xét tam giác ABC và tam giác ADE có:

AE=AC(cmt) 

EAC: chung

AB=AD(gt) 

=>Tam giác ABC=tam giác ADE(c.g.c)

=>đpcm

Ta có : AE=AB+BE                                                                                                                                              AC=AD+DC                                                                                                                                              Mà BE=DC và AB=AD\(\Rightarrow\) AE=AC

      Xét tam giác ABC và tam giác ADE                                                                                                                  có:   AC=AE (cmt)                                                                                                                                           góc A chung                                                                                                                                            AB=AD (gt)                                                                                                                                           \(\Rightarrow\) Tam giác ABC=Tam giác ADE (c.g.c)                                                                                             Tích đúng cho mình nha !

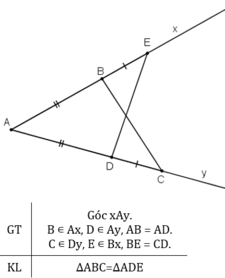
Ta có: AB = AD, BE = DC ⇒ AB + BE = AD + DC hay AE = AC.

Xét ΔABC và Δ ADE có:

    AC = AE (cmt)

    Góc A chung

    AB = AD (gt)

⇒ ΔABC = ΔADE (c.g.c)

Tự vẽ hình 

Xét tam giác ABC và tam giác ADE , ta có:

AB = AD (1) (gt)

EB = DC ; AB = AD => AB + BE = AD+DC nên AE = AC (2) (gt)

Góc A chung (3)

Từ (1) ; (2) ; (3) => \(\Delta ABC=\Delta ADE\)

sorry, em mới học lớp 6 thui

Điều kiện: xOy < 180^o

Ta có hình vẽ:

Vì AB = AD (gt), BE = DC (gt)

=> AB + BE = AD + DC

hay AE = AC

Xét Δ ABC và Δ ADE có:

AC = AE (chứng minh trên)

A là góc chung

AB = AD (gt)

Do đó, Δ ABC = Δ ADE (c.g.c) (đpcm)

Ta có hình vẽ:

GT: \(\widehat{xAy}\) ; B ϵ Ax ; C ϵ Ay ; AB = AD

       E ϵ Bx ; C ϵ Dy ; BE = DC

KL: ΔABC = ΔADE

Xét ΔABC và ΔADE có:

AC=AE (gt)

A là góc chung

BE =DC (gt)

=>  ΔABC = ΔADE (cạnh - góc - cạnh) (đpcm)