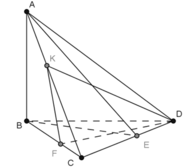
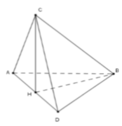
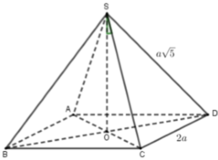
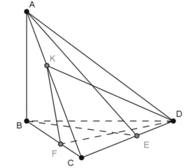
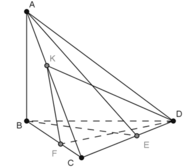
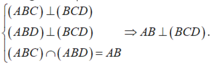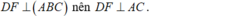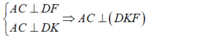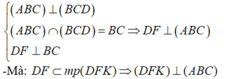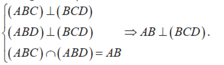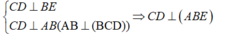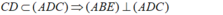Cho tứ diện ABCD gọi a1 là góc hợp bởi 2 mặt phẳng(ABD) và (ABC), a2 là góc hợp bởi 2 mp (ACD) và (ABC), a3 là góc hợp bởi 2 mp (ACD) và (ABD), a4 là góc hợp bởi 2 mp (ACD) và (BCD), a5 là góc hợp bởi 2 mp (ABD) và (BCD), a6 là góc hợp bởi 2 mp (ABC) và (BCD). Chứng minh với mọi số thực x,y,z,t \(\in R\)thỏa mãn \(^{x^2+y^2+z^2+t^2}\)
Ta có : z.t.cos(a1)+t.y.cos(a2)+y.z.cos(a3)+x.y.cos(a4)+x.z.cos(a5)+x.t.cos(a6) =<\(\frac{1}{2}\) (\(x^2+y^2+z^2+t^2\))