1.Đại lượng y là hàm số của đại lượng x vì ta có mỗi giá trị của đại lượng x đều có một giá trị tương ứng của đại lượng y . Giá trị tương ứng ấy của đại lượng y là duy nhất.

2. Đại lượng y không phải là hàm số của đại lượng x vì ứng với giá trị x = 5 chẳng hạn ta có hai giá trị của y (ước tự nhiên của 5 là 1 và 5)

3. Dựa vào định nghĩa các phép toán về số hữu tỉ. Chú ý rằng với các số hữu tỉ thì kết quả của các phép toán này là số hữu tỉ. Chẳng hạn câu b). Giả sử tích của số hữu tỉ \(x\ne0\)với số vô tỉ y là số hữu tỉ z. Ta có x.y=z.

Như vậy thì \(y=\frac{z}{x}\). Nhưng z và x \(\left(x\ne0\right)\)là hai số hữu tỉ nên thương của chúng cũng là số hữu tỉ. Suy ra y là số hữu tỉ, trái với đề bài. Vậy tích của một số hữu tỉ khác 0 với một số vô tỉ là một số vô tỉ.

Vẽ hình:

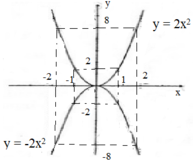
Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0

Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.

Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.

Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.

Vẽ hình:

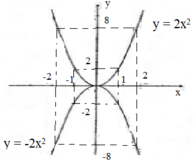
a) Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0

Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.

Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.

Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.

b) Đồ thị hàm số y = a x 2  là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.

Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).

Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.

a) khi m khác 1/2

b)khi m >1

c) khi K<5

Bài 1:

Hàm số y=(m-3)x+4 đồng biến trên R khi m-3>0

=>m>3

Hàm số y=(m-3)x+4 nghịch biến trên R khi m-3<0

=>m<3

Bài 4:

a: Vì \(a=3-\sqrt{2}>0\)

nên hàm số \(y=\left(3-\sqrt{2}\right)x+1\) đồng biến trên R

b: Khi x=0 thì \(y=0\left(3-\sqrt{2}\right)+1=1\)

Khi x=1 thì \(y=\left(3-\sqrt{2}\right)\cdot1+1=3-\sqrt{2}+1=4-\sqrt{2}\)

Khi \(x=\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\cdot\sqrt{2}+1=3\sqrt{2}-2+1=3\sqrt{2}-1\)

Khi \(x=3+\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)-1\)

=9-4-1

=9-5

=4

Khi \(x=3-\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)^2-1\)

\(=11-6\sqrt{2}-1=10-6\sqrt{2}\)

a: Để (1) là hàm số bậc nhất thì \(m-2\ne0\)

=>\(m\ne2\)

b: Để (1) đồng biến thì m-2>0

=>m>2

c: Khi m=1 thì \(y=\left(1-2\right)x+1+1=-x+2\)

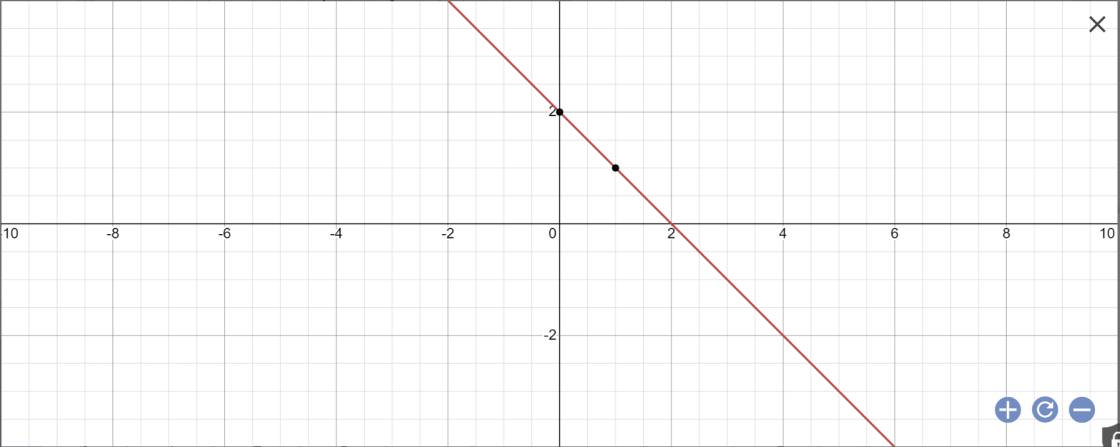
d: Thay x=2 và y=1 vào (1), ta được:

\(2\left(m-2\right)+m+1=1\)

=>2m-4+m=0

=>3m-4=0

=>3m=4

=>\(m=\dfrac{4}{3}\)

e: Để (1)//y=3x+2 thì \(\left\{{}\begin{matrix}m-2=3\\m+1< >2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m=3\\m< >1\end{matrix}\right.\)

=>m=3

f: Để (1) tạo với trục Ox một góc tù thì m-2<0

=>m<2

g: Thay x=0 vào y=5x+6, ta được:

\(y=5\cdot0+6=6\)

Thay x=0 và y=6 vào (1), ta được:

\(0\left(m-2\right)+m+1=6\)

=>m+1=6

=>m=5

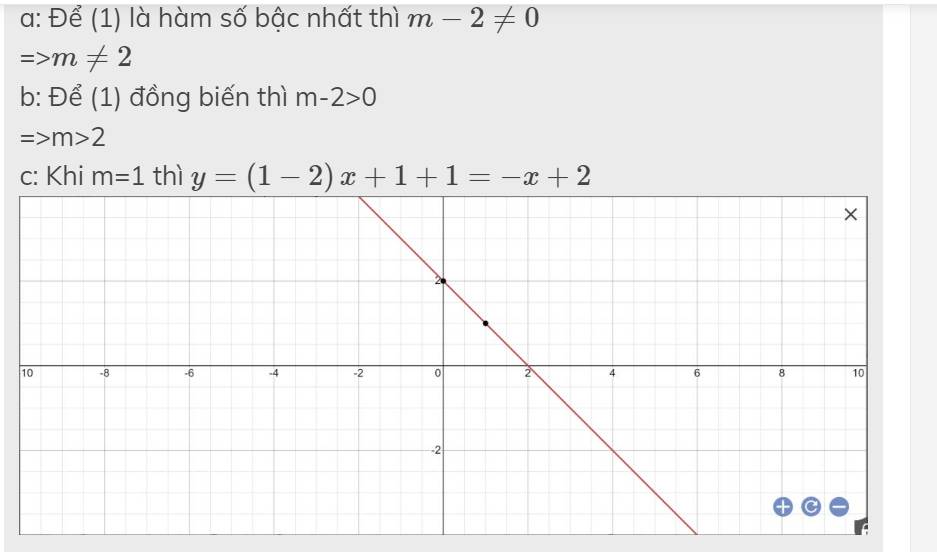
h: Khi m=3 thì \(y=\left(3-2\right)x+3+1=x+4\)

Gọi \(\alpha\) là góc tạo bởi đồ thị hàm số y=x+4 với trục Ox

\(tan\alpha=a=1\)

=>\(\alpha=45^0\)

y=x+4

=>x-y+4=0

Khoảng cách từ O(0;0) đến đường thẳng x-y+4=0 là:

\(\dfrac{\left|0\cdot1+0\cdot\left(-1\right)+4\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{4}{\sqrt{2}}=2\sqrt{2}\)

\(a,\Leftrightarrow\dfrac{m-1}{m+1}\ne0\Leftrightarrow m\ne\pm1\\ b,\Leftrightarrow\dfrac{m-1}{m+1}>0\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\\ c,\Leftrightarrow\dfrac{m-1}{m+1}+m+2=2\\ \Leftrightarrow\dfrac{m-1+m^2+m}{m+1}=0\\ \Leftrightarrow m^2+2m-1=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-1+\sqrt{2}\\m=-1-\sqrt{2}\end{matrix}\right.\)