Cho hàm số y=x²(P) và hàm số y=x+m(d). Tìm các giá trị của m để (d) tiếp xúc với (P). Tìm toạ độ tiếp điểm. Giúp em với ạ, ngay bây giờ luôn nhé. Em đang tự ôn thi tuyển sinh:(((
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 5 2021
a) vẽ bạn tự vẽ nha
b) Xét pt hoành độ giao điểm chung của (d) và (P) ta có:
\(\frac{1}{4}x^2=x+m\)
\(\Leftrightarrow x^2-4x-4m=0\left(1\right)\)
\(\Delta^,=4+4m\)
Để (d) tiếp xúc với (P) \(\Leftrightarrow\Delta^,=0\)
\(\Leftrightarrow4+4m=0\)
\(\Leftrightarrow m=-1\)
Thay m=-1 vào pt (1) ta được :
\(x^2-4x+4=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x=2\)
\(\Rightarrow y=\frac{1}{4}.2^2=1\)
Gọi tọa độ tiếp điểm của (d) tiếp xúc với (P) là A(x,y)
=> tọa độ tiếp điểm là \(A\left(2;1\right)\)
14 tháng 4 2022
a: Để hàm số đồng biến thì 2m-6>0
hay m>3
b: Phương trình hoành độ giao điểm là:
\(x^2-\left(2m-6\right)x-m+9=0\)
\(\text{Δ}=\left(2m-6\right)^2-4\left(-m+9\right)\)
\(=4m^2-24m+36+4m-36\)
=4m2-20m
Để (P) tiếp xúc với (d) thì 4m(m-5)=0
=>m=0 hoặc m=5
26 tháng 9 2021
Bài 2:
a: Phương trình hoành độ giao điểm là:
x-2=2-x
\(\Leftrightarrow2x=4\)
hay x=2
Thay x=2 vào (d1), ta được:
y=2-2=0
Thay x=2 và y=0 vào (d3), ta được:
2(2-m)+1=0
\(\Leftrightarrow4-2m+1=0\)
hay \(m=\dfrac{5}{2}\)
KT
6 tháng 1 2019
Bài 1:
Đặt: (d): y = (m+5)x + 2m - 10
Để y là hàm số bậc nhất thì: m + 5 # 0 <=> m # -5
Để y là hàm số đồng biến thì: m + 5 > 0 <=> m > -5
(d) đi qua A(2,3) nên ta có:
3 = (m+5).2 + 2m - 10
<=> 2m + 10 + 2m - 10 = 3
<=> 4m = 3
<=> m = 3/4
KT
6 tháng 1 2019
(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:
9 = (m+5).0 + 2m - 10
<=> 2m - 10 = 9
<=> 2m = 19
<=> m = 19/2
(d) đi qua điểm 10 trên trục hoành nên ta có:
0 = (m+5).10 + 2m - 10
<=> 10m + 50 + 2m - 10 = 0
<=> 12m = -40
<=> m = -10/3
(d) // y = 2x - 1 nên ta có:
\(\hept{\begin{cases}m+5=2\\2m-10\ne-1\end{cases}}\) <=> \(\hept{\begin{cases}m=-3\\m\ne\frac{9}{2}\end{cases}}\) <=> \(m=-3\)
21 tháng 3 2022
Phương trình hoành độ giao điểm là:
Để phương trình có hai nghiệm phân biệt thì Δ>0
Gửi anh :)
A
5 tháng 1 2019
a,phương trình hoành độ giao điểm của (P) và (D) là:
x2 = mx - m + 1 (1) \(\Leftrightarrow\) x2 - mx + m - 1 = 0
\(\Delta\) = m2 - 4m +4 = (m - 20)2\(\ge\)0 với mọi giá trị của m
\(\Rightarrow\) phương trình (1) luôn luôn có nghiệm hay (D) và (P) luôn luôn có điểm chung voeí mọi giá trị của m
b,(D) tiếp xúc với (P) khi (1) có nghiệm kép hay :
\(\Delta\) = ( m - 2 )2 = 0 \(\Leftrightarrow\) m = 2
lúc đó phương trình củađường thẳng (D) là : y = 2x -1
c, tự vẽ đồ thị nha
trên đồ thị ta thấy (P) và (D) tiếp xúc nhau tại điểm A (1;1)
KV
27 tháng 4 2023
Phương trình hoành độ giao điểm của (P) và (d):
x² = 2x + m
⇔ x² - 2x - m = 0
∆ = (-2)² - 4.1.(-m)
= 4 + 4m
Để (P) và (d) tiếp xúc thì phương trình hoành độ giao điểm của (P) và (d) có nghiệm kép
⇔ ∆ = 0
⇔ 4 + 4m = 0
⇔ 4m = -4
⇔ m = -1
Vậy m = -1 thì (P) và (d) tiếp xúc
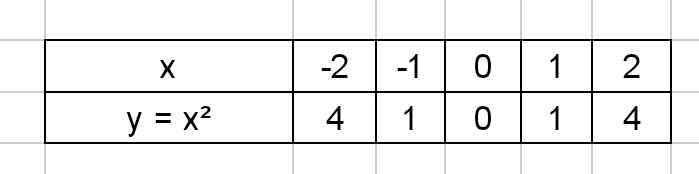
Phương trình hoành độ giao điểm:
\(x^2=x+m\Leftrightarrow x^2-x-m=0\) (1)
(P) tiếp xúc (d) khi và chỉ khi (1) có nghiệm kép
\(\Leftrightarrow\Delta=1+4m=0\Rightarrow m=-\dfrac{1}{4}\)
Khi đó hoành độ giao điểm là: \(x=-\dfrac{-1}{2}=\dfrac{1}{2}\Rightarrow y=\dfrac{1}{4}\)
Tọa độ tiếp điểm: \(\left(\dfrac{1}{2};\dfrac{1}{4}\right)\)