1) Cho tam giác ABC . M là điểm nằm trong tam giác ABC đường thẳng qua M song song với AC cắt BC tại D , đường thẳng qua M song song với BC cắt AB tại E , đường thẳng qua M song song với AB cắt AC tại F .
a) chứng minh : các tứ giác BEMD , AFME ,DMFC là các hình thang cân .
b) độ dài các đoạn thẳng MA ,MB ,MC bằng độ dài ba cạnh của một tam giác nào đó
2) cho hình thang ABCD (AB//DC) trong đó 2 tia phân giác của góc A và góc B cắt nhau tại K thuộc đáy ĐC .
C/m : AD + BC = CD


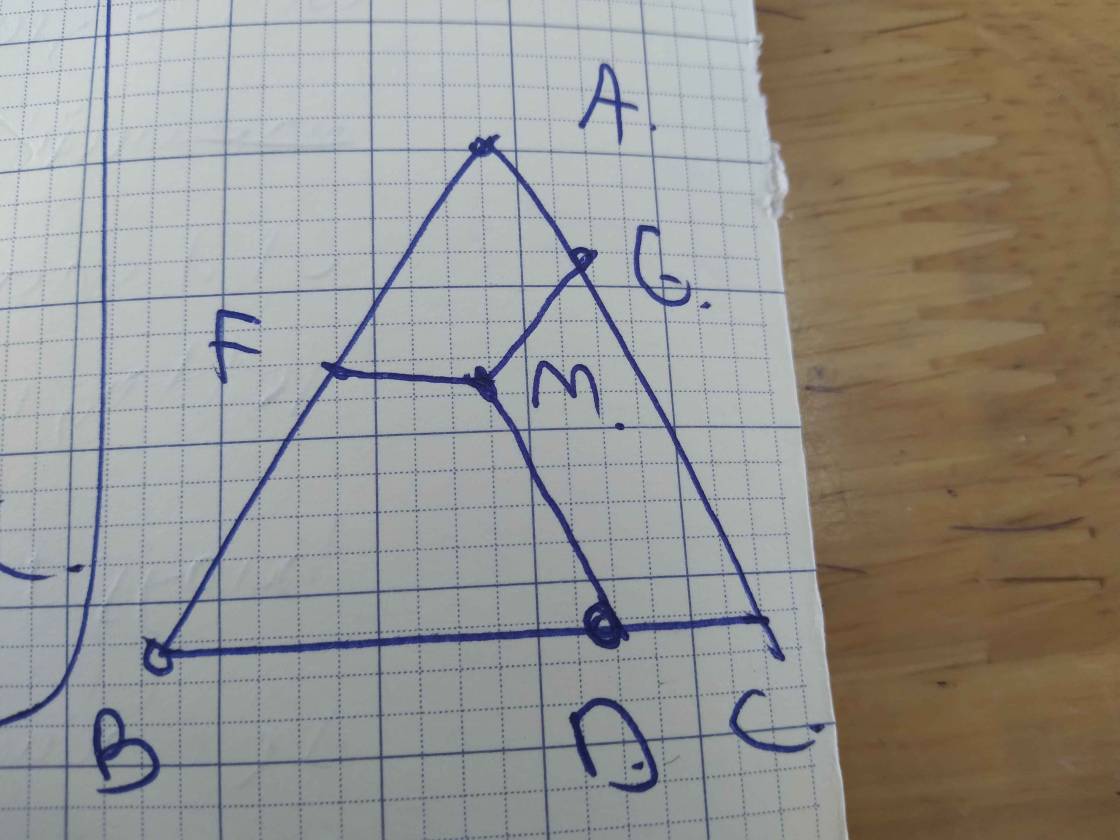



bài 1 sai đề rồi bạn. Nếu BEMD là ht cân thật thì \(\widehat{ABC}=\widehat{MDB}\)mà \(\widehat{MDB}=\widehat{ACB}\)(đồng vị) => \(\widehat{ABC}=\widehat{ACB}\)=> tam giác ABC cân( trái với đề bài)
Nhưng ngta đâu có ns là tam giác ABC ko đc cân đâu :3