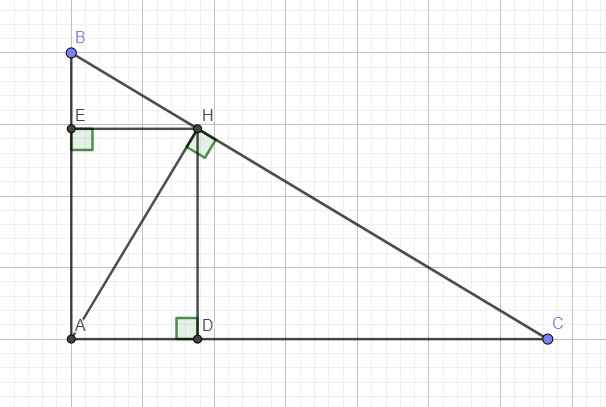
cho tam giác abc vuông tại a đường cao ah . Từ h kẻ hd và he lần lượt vuông góc với ab,ac. giả sử diện tích tam giác abc=2 diện tích tam giác adhe chứng minh rằng tam giác abc vuông cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: AC=20cm
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{15\cdot20}{2}=150\left(cm^2\right)\)
2: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
Do đó: ADHE là hình chữ nhật
3: Xét tứ giác AFDH có
AF//DH
AF=DH
Do đó: AFDH là hình bình hành

a: Xét tứ giác ADHE có
góc ADH=góc AEH=góc DAE=90 độ
nên ADHE là hình chữ nhật
b: ADHE là hình chữ nhật
nen AH=DE
c: Để ADHE là hình vuông thì AH là phân giác của góc DAE
=>ΔABC cân tại A
=>AB=AC

Ta có tứ giác ADHE là hình chữ nhật (tứ giác có 4 góc vuông)
\(\Rightarrow S_{ADHE}=AD.HD\le\dfrac{1}{2}\left(AD^2+HD^2\right)=\dfrac{1}{2}AH^2\)
Mà theo hệ thức lượng: \(AH^2=BH.CH\)
\(\Rightarrow S_{ADHE}\le\dfrac{1}{2}BH.CH\le\dfrac{1}{8}\left(BH+CH\right)^2=\dfrac{1}{8}BC^2=2\left(cm^2\right)\)
Vậy \(S_{ADHE-max}=2\left(cm^2\right)\) khi tam giác ABC vuông cân tại A