Bạn ơi, đề câu a sai nhé ! Mình đọc không có điểm I nha !

a) Xét tứ giác AMND có 

AM//DN

AM=DN

Do đó: AMND là hình bình hành

Suy ra: AD=NM

b) Xét tứ giác BCNM có 

BM//CN

BM=CN

Do đó: BCNM là hình bình hành

a: Xét tứ giác BMDN có 

BM//ND

BM=ND

Do đó: BMDN là hình bình hành

Suy ra: MD//BN

a: Xét tứ giác BMDN có 

BM//DN

BM=DN

Do đó: BMDN là hình bình hành

Suy ra: MD//BN và MD=BN(2)

b: Xét tứ giác AMND có 

AM//ND

AM=ND

Do đó: AMND là hình bình hành

Suy ra: I là trung điểm của MD

hay \(MI=\dfrac{MD}{2}\)(1)

Xét tứ giác BMNC có

BM//NC

BM=NC

Do đó: BMNC là hình bình hành

Suy ra: K là trung điểm của BN

hay \(NK=\dfrac{BN}{2}\left(3\right)\)

Từ (1), (2) và (3) suy ra MI//NK và MI=NK

hay INKM là hình bình hành

a: Xét tứ giác BMDN có 

BM//DN

BM=DN

Do đó: BMDN là hình bình hành

Suy ra: MD//BN

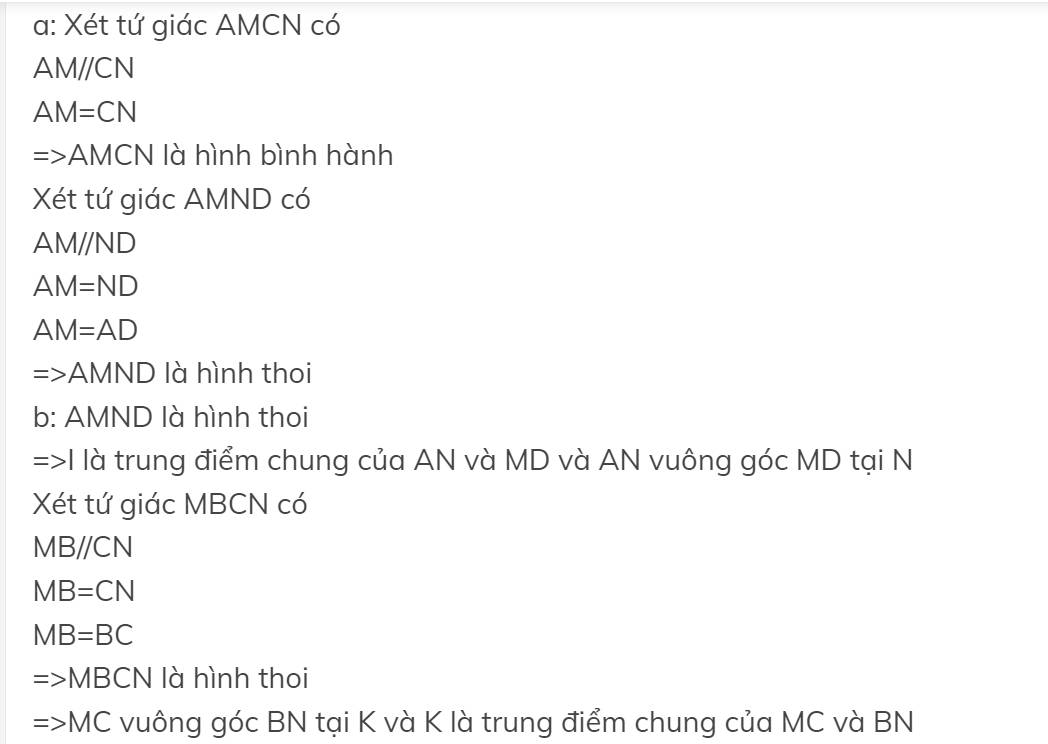
a: Xét tứ giác AMCN có

AM//CN

AM=CN

=>AMCN là hình bình hành

Xét tứ giác AMND có

AM//ND

AM=ND

AM=AD

=>AMND là hình thoi

b: AMND là hình thoi

=>I là trung điểm chung của AN và MD và AN vuông góc MD tại N

Xét tứ giác MBCN có

MB//CN

MB=CN

MB=BC

=>MBCN là hình thoi

=>MC vuông góc BN tại K và K là trung điểm chung của MC và BN

Xét ΔMDC có

MN là trung tuyến

MN=DC/2

=>ΔMDC vuông tại M

Xét tứ giác MINK có

góc MIN=góc MKN=góc IMK=90 độ

=>MINK là hình chữ nhật

c: Xét ΔMDC có MI/MD=MK/MC

nên IK//DC