Cho tam giác ABC , M là trung điểm của BC . Trên tia đối của tia MA lấy điểm D sao cho MA = MD . Chứng minh rằng :
a , Tam giác ABM = tam giác DCM .
b , AB song song với CD
c, Kẻ BE vuông góc với AM ( E thuộc AM ) , kẻ CF vuông góc với DM ( F thuộc DM )
Chứng minh rằng M là trung điểm của đoạn thẳng EF
giúp mik nha tối chủ nhật mik chép đấy , nhớ nha mik tick cho đừng viết tắt

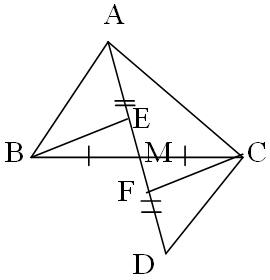
Hình mik vẽ không có đo nên các trung điểm mik lấy đại, có thể hơi lêch một tí.
a, Xét tam giác ABM và tam giác DCM
Ta có: AM = DM ( giả thiết)
góc AMB = góc AMC ( đối đỉnh)
BM = CM ( M là trung điểm BC)
Do đó: tam giác ABM = tam giác DCM ( c-g-c)
b, Ta có: tam giác ABM = tam giác DCM ( chứng minh trên)
góc ABM = góc DCM
Mà hai góc này nằm ở vị trí so le trong.
Suy ra: AB // CD
c,Xét tam giác BEM và tam giác CFM
Ta có: góc EMB = góc FMC ( đối đỉnh)
BM = CM ( M là trung điểm BC)
góc BEM = góc CFM = 90 độ ( BE vuông góc AM, CF vuông góc DM)
Do đó: tam giác BEM = tam giác CFM( cạnh huyền, góc nhọn)
Suy ra: EM = FM
Mà E, F, M thẳng hàng ( cùng thuộc AD)
Vậy M là trung điểm EF.