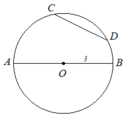
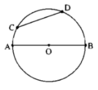
Cho đường tròn (O) tâm O đường kính AB. Lấy hai điểm phân biệt C và D thuộc đường tròn (O); biết C và D nằm khác phía đốt với đường thẳng AB. Gọi E,F tương ứng là trung điểm của hai dây AC, AD.
1) Chứng minh AC^2 + CB^2 = AD^2 + DB^2.
2) chứng minh tứ giác AEOF nội tiếp đường tròn. Xác định tâm đường tròn ngoại tiếp tứ giác AEOF.
3) Đường thẳng EF cắt đường tròn ngoại tiếp ADE tại điểm K khác E.
Chứng minh đường thẳng DK là tiếp tuyến của đường tròn (O). Tìm điều kiện của tam giác ACD để tứ giácAEDK là hình chữ nhật