y x 3 + y x 5 + y x 2 = 900
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: \(-3x=7y=21z\)
\(\Rightarrow-3x\cdot\frac{1}{21}=7y\cdot\frac{1}{21}=21z\cdot\frac{1}{21}\)
\(\Rightarrow\frac{x}{-7}=\frac{y}{3}=\frac{z}{1}=\frac{5x}{-35}=\frac{10y}{30}=\frac{6z}{6}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{5x}{-35}=\frac{10y}{30}=\frac{6z}{6}=\frac{5x+10y+6z}{-35+30+6}=\frac{4}{1}=4\)
\(\Rightarrow\hept{\begin{cases}\frac{5x}{-35}=4\rightarrow5x=-140\rightarrow x=-28\\\frac{10y}{30}=4\rightarrow10y=120\rightarrow y=12\\\frac{6z}{6}=4\rightarrow z=4\end{cases}}\)
Vậy x= -28; y=12; z=4
b) Ta có: \(\hept{\begin{cases}\frac{x}{2}=\frac{y}{5}\rightarrow\frac{x}{6}=\frac{y}{15}\\\frac{y}{3}=\frac{z}{20}\rightarrow\frac{y}{15}=\frac{z}{100}\end{cases}}\)
\(\Rightarrow\frac{x}{6}=\frac{y}{15}=\frac{z}{100}\)
Đặt \(\frac{x}{6}=\frac{y}{15}=\frac{z}{100}=k\)
\(\Rightarrow x=6k;y=15k;z=100k\)
\(y\cdot z=900\rightarrow15k\cdot100k=900\)
\(\rightarrow1500\cdot k^2=900\)
\(\rightarrow k^2=\frac{3}{5}\rightarrow k\varepsilon\varnothing\)
Vậy x;y;z ko có giá trị thỏa mãn
c) Ta có: \(\frac{x}{2}=\frac{y}{5}=\frac{x^2}{4}=\frac{y}{25}^2\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x^2}{4}=\frac{y^2}{25}=\frac{x^2+y^2}{4+25}=\frac{116}{29}=4\)
\(\Rightarrow\hept{\begin{cases}\frac{x^2}{4}=4\rightarrow x^2=16\rightarrow\orbr{\begin{cases}x=4\\x=-4\end{cases}}\\\frac{y^2}{25}=4\rightarrow y^2=100\rightarrow\orbr{\begin{cases}y=10\\y=-10\end{cases}}\end{cases}}\)\(\Rightarrow\frac{x^2}{4}=4\rightarrow x^2=16\rightarrow\orbr{\begin{cases}x=4\\x=-4\end{cases}}\)
\(\frac{y^2}{25}=4\rightarrow y^2=100\rightarrow\orbr{\begin{cases}y=10\\y=-10\end{cases}}\)
Vậy (x;y) = (4;10); (-4;-10)

Câu 3:
\(\dfrac{x}{y}=\dfrac{5}{9}\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{5}=\dfrac{y}{9}=\dfrac{x-y}{5-9}=\dfrac{-40}{-4}=10\)
\(\dfrac{x}{5}=10\Rightarrow x=5\\ \dfrac{y}{9}=10\Rightarrow y=90\)
Câu b:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{5x-2y}{10-6}=\dfrac{28}{4}=7\)
\(\dfrac{x}{2}=7\Rightarrow x=14\\ \dfrac{y}{3}=7\Rightarrow y=21\)
Câu c:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{5}=\dfrac{y}{7}=\dfrac{z}{10}=\dfrac{x+y-1}{5+7-10}=\dfrac{20}{2}=10\)
\(\dfrac{x}{5}=10\Rightarrow x=50\\ \dfrac{y}{7}=10\Rightarrow y=70\\ \dfrac{z}{10}=10\Rightarrow z=100\)
Câu d:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{3x-2y+2z}{9-8+10}=\dfrac{121}{11}=11\)
\(\dfrac{x}{3}=11\Rightarrow x=3\\ \dfrac{y}{4}=11\Rightarrow y=44\\ \dfrac{z}{5}=11\Rightarrow z=55\)
Câu e:
\(\dfrac{x}{4}=\dfrac{y}{2}\Rightarrow\dfrac{x}{8}=\dfrac{y}{6}\\\dfrac{y}{3}=\dfrac{z}{5}\Rightarrow\dfrac{y}{6}=\dfrac{z}{10}\\ \Rightarrow\dfrac{x}{8}=\dfrac{y}{6}=\dfrac{z}{10} \)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{8}=\dfrac{y}{6}=\dfrac{z}{10}=\dfrac{x+y-z}{8+6-10}=\dfrac{20}{4}=5\)
\(\dfrac{x}{8}=5\Rightarrow x=40\\ \dfrac{y}{6}=5\Rightarrow y=30\\ \dfrac{z}{10}=5\Rightarrow z=50\)
3) \(\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}=\dfrac{x-y}{5-9}=\dfrac{-40}{-4}=10\)
\(\Rightarrow\left\{{}\begin{matrix}x=10.5=50\\y=10.9=90\end{matrix}\right.\)
4) \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{5x}{10}=\dfrac{2y}{6}=\dfrac{5x-2y}{10-6}=\dfrac{28}{4}=7\)
\(\Rightarrow\left\{{}\begin{matrix}x=7.2=14\\y=7.3=21\end{matrix}\right.\)
5) \(\dfrac{x}{5}=\dfrac{y}{7}=\dfrac{z}{10}=\dfrac{x+y-z}{5+7-10}=\dfrac{20}{2}=10\)
\(\Rightarrow\left\{{}\begin{matrix}x=10.5=50\\y=10.7=70\\z=10.10=100\end{matrix}\right.\)
6) \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{3x}{9}=\dfrac{2y}{8}=\dfrac{2z}{10}=\dfrac{3x-2y+2z}{9-8+10}=\dfrac{121}{11}=11\)
\(\Rightarrow\left\{{}\begin{matrix}x=11.3=33\\y=11.4=44\\z=11.5=55\end{matrix}\right.\)
7) \(\Rightarrow\dfrac{x}{12}=\dfrac{y}{6}=\dfrac{z}{10}=\dfrac{x+y-z}{12+6-10}=\dfrac{20}{8}=\dfrac{5}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}.12=30\\y=\dfrac{5}{2}.6=15\\z=\dfrac{5}{2}.10=25\end{matrix}\right.\)

a: =2(x-y)^3/(x-y)-7(x-y)^2/(x-y)+(x-y)/(x-y)
=2(x-y)^2-7(x-y)+1
b: =3(x-y)^5/5(x-y)^2-2(x-y)^4/5(x-y)^2+3(x-y)^2/5(x-y)^2
=3/5(x-y)^3-2/5(x-y)^2+3/5
\(a,\)
\(\left[2\left(x-y\right)^3-7\left(y-x\right)^2-\left(y-x\right)\right]:\left(x-y\right)\)
\(=\left[2\left(x-y\right)^3-7\left(x-y\right)^2+\left(x-y\right)\right]:\left(x-y\right)\)
\(=\left\{\left(x-y\right)\left[2\left(x-y\right)^2-7\left(x-y\right)+1\right]\right\}:\left(x-y\right)\)
\(=2\left(x-y\right)^2-7\left(x-y\right)+1\)
\(b,\)
\(\left[3\left(x-y\right)^5-2\left(x-y\right)^4+3\left(x-y\right)^2\right]:\left[5\left(x-y\right)^2\right]\)
\(=\dfrac{3}{5}\left(x-y\right)^3-\dfrac{2}{5}\left(x-y\right)^2+\dfrac{3}{5}\)

b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x+y}{3+5}=\dfrac{-32}{8}=-4\)
Do đó: x=-12; y=-20

1) \(x+y=10\) mà \(x=y\) nên: \(x=y=\dfrac{10}{2}=5\)
2) \(2x+3y=180\) mà \(x=y\)
Ta có: \(2y+3y=180\Rightarrow5y=180\Rightarrow y=180:5=36\)
Vậy \(x=y=36\)
3) \(x+y=180\) mà \(x=y\) nên: \(x=y=\dfrac{180}{2}=90\)
4) \(3x+5y=13\) mà \(y=2x\) ta có:
\(3x+5\cdot2x=13\Rightarrow13x=13\Rightarrow x=1\)
\(y=2x=2\cdot1=2\)
Các câu còn lại bạn làm tương tự

`@` `\text {Ans}`
`\downarrow`
`1,`
\((y-5)(y+8)-(y+4)(y-1)\)
`= y(y+8) - 5(y+8) - [y(y-1) + 4(y-1)]`
`= y^2+8y - 5y - 40 - (y^2-y + 4y - 4)`
`= y^2+8y-5y-40 - y^2+y-4y+4`
`= (y^2-y^2)+(8y-5y+y-4y) +(-40+4)`
`= -36`
Vậy, bt trên không phụ thuộc vào gtr của biến.
`2,`
\(y^4-(y^2+1)(y^2-1)\)
`= y^4 - [y^2(y^2-1)+y^2-1]`
`= y^4- (y^4-y^2 + y^2-1)`
`= y^4-(y^4-1)`
`= y^4-y^4+1`
`= 1`
Vậy, bt trên không phụ thuộc vào gtr của biến.
`3,`
\(x(y-z) + y(z-x) +z(x-y)\)
`= xy-xz + yz - yx + zx-zy`
`= (xy-yx) + (-xz+zx) + (yz-zy)`
`= 0`
Vậy, bt trên không phụ thuộc vào gtr của biến.
`4,`
\(x(y+z-yz) -y(z+x-xz)+z(y-x)\)
`= xy+xz-xyz - yz - yx + yxz + zy - zx`
`= (xy-yx)+(xz-zx)+(-xyz+yxz)+(-yz+zy)`
`= 0`
Vậy, bt trên không phụ thuộc vào gtr của biến.
`5,`
\(x(2x+1)-x^2(x+2)+x^3-x+3\)
`= 2x^2+x - x^3 - 2x^2 + x^3 - x + 3`
`= (2x^2-2x^2)+(-x^3+x^3)+(x-x)+3`
`= 3`
Vậy, bt trên không phụ thuộc vào gtr của biến.
`6,`
\(x(3x-x+5)-(2x^3+3x-16)-x(x^2-x+2)\)
`= 3x^2 - x^2 + 5x - 2x^3 - 3x + 16 - x^3 + x^2 - 2x`
`= -3x^3 + 3x^2 + 16`
Bạn xem lại đề bài.
`\text {#KaizuulvG}`
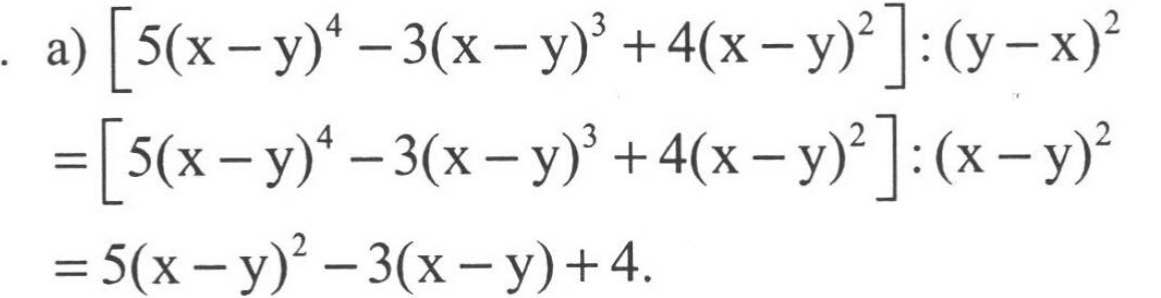
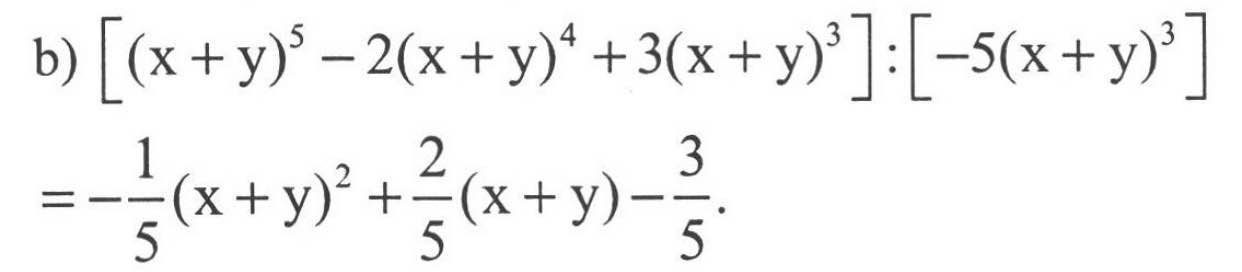
y x 3 + y x 5 + y x 2 = 900
y x ( 3 + 5 + 2 ) = 900
y x 9 = 900
y = 900 : 9
y = 100
Vậy y = 100
y x 3 + y x 5 + y x 2 = 900
y x ( 3 + 5 + 2 ) = 900
y x 10 = 900
y = 900 / 10
y = 90