chứng minh rằng ab+ba chia hết cho 11.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 2 2022
a)ab+ba
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b+10b+a
= 11a + 11b
Ta thấy: 11a⋮11 ; 11b⋮11
=>ab+ba⋮11 (ĐPCM)
b)ab-ba⋮9
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b-10b+a
= 9a - 9b
Ta thấy: 9a⋮9 ; 9b⋮9
=>ab+ba⋮9 (ĐPCM)
PT
1
CM
6 tháng 7 2018
a, a b + b a = (10a+b)+(10b+a) = 11a+11b = 11.(a+b) ⋮ 11
b, a b - b a = (10a+b) - (10b+a) = 9a - 9b = 9(a - b) ⋮ 9 (a>b)
NT
1
16 tháng 2 2022
a)ab+ba
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b+10b+a
= 11a + 11b
Ta thấy: 11a⋮11 ; 11b⋮11
=>ab+ba⋮11 (ĐPCM)
b)ab-ba⋮9
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b-10b+a
= 9a - 9b
Ta thấy: 9a⋮9 ; 9b⋮9
=>ab+ba⋮9 (ĐPCM)
16 tháng 2 2022
b) ab+ba
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b+10b+a
= 11a + 11b
Ta thấy: 11a⋮11 ; 11b⋮11
=>ab+ba⋮11 (ĐPCM)
1 tháng 3 2023
Theo đề bài ra, ta có :
`ab` `+` `ba` `=` `10a` `+` `b` `+` `10b` `+ a`
`=` `11a` `+` `11b`
`=` `11` `(a+b)`
\(\rightarrow\) `11` `(a+b)` chia hết cho `11`
\(\Rightarrow\) `ab` `+` `ba` chia hết cho `11`
@Nae
16 tháng 2 2022
b)ab+ba
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b+10b+a
= 11a + 11b
Ta thấy: 11a⋮11 ; 11b⋮11
=>ab+ba⋮11 (ĐPCM)
NV
3
25 tháng 2 2023
Ta có : \(\overline{ab}+\overline{ba}\text{=}10a+b+10b+a\)
\(\text{=}\left(10a+a\right)+\left(10b+b\right)\)
\(\text{=}11a+11b\)
\(\text{=}11\left(a+b\right)\)
\(\Rightarrow\overline{ab}+\overline{ba}⋮11\)
25 tháng 2 2023
Ta có :
ab=a.10+b.1
ba=b.10+a.1
⇒ab+ba=a.11+b.11
⇒ab+ba=11.(a+b)
Vì 11⋮11 ⇒ 11.(a+b)
⇒11.(a+b) ⋮ 11
⇒(ab+ba)⋮ 11
Vậy(ab+ba)⋮11
TQ
3
SN
28 tháng 6 2015
đặt c = a+ b
ta có: ab¯ + ba¯ =cc¯
mà cc¯ chia hết cho 11 ( cc¯:11=c)
ab=10*a+b
ba=10*b+a
ab-ba=9*a-9*b=9*(a-b)=> ab-ba chia hết cho 9
27 tháng 9 2016
ab+ba=10a + b +10b + a = 11a + 11b = 11 (a+b) chia hết cho 111
tớ chỉ giải đc 1 câu thôi còn câu b tịt
30 tháng 11 2015
ab + ba = ( 10a +1b ) + ( 10b + 1a )
= 11a + 11b chia hết cho 11
Suy ra ab + ba cha hết cho 11
16 tháng 2 2022
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b+10b+a
= 11a + 11b
Ta thấy: 11a⋮11 ; 11b⋮11
=>ab+ba⋮11 (ĐPCM)
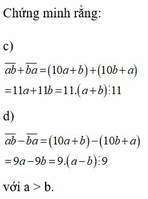
ab+ba=10a+b+10b+a=11a+11b chia hết cho 11
Ta có : ab + ba = a x 10 + b + b x 10 + a
= a x 11 + b x 11
= (a+b) x 11
Vậy chắc chắn nó chia hết cho 11 l i k e t