Trong các hàm số sau, những hàm sô nào luôn đồng biến trên từng khoảng xác định của nó
y= 2x+1/x+3 (I)
y=-x^4+2x^2+1(II)
y=3x^3+x-3(III)
A. (I) và (III)
b.(I)
c.(II) va (III)
d.(I) va(III)
giải chi tiết ra giúp e ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Hàm số (I): ![]() , ∀x ∈ D = R \ {-1} nên hàm số đồng biến trên từng khoảng xác định của nó.
, ∀x ∈ D = R \ {-1} nên hàm số đồng biến trên từng khoảng xác định của nó.
Hàm số (II): y’ = -4x3 + 2x. y' = 0 <=> - 4x3 + 2x = 0 <=> 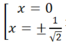 nên hàm số không đồng biến trên khoảng xác định của nó.
nên hàm số không đồng biến trên khoảng xác định của nó.
Hàm số (III): y’ = 3x2 – 3.
y’ = 0 <=> 3x2 – 3 = 0 <=> x = ±1 nên hàm số không đồng biến trên khoảng xác định của nó.

Chọn B
Hàm số đồng biến khi a > 1.
Viết lại các hàm số về dạng hàm số mũ y = a x :
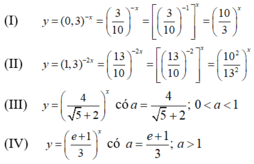
Trong bốn cơ số ta thấy chỉ có hai cơ số lớn hơn 1 là
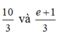
Do đó chỉ có hai hàm số (I) và (IV) là đồng biến trên R
\(y=\dfrac{2x+1}{x+3}\Rightarrow y'=\dfrac{5}{\left(x+3\right)^2}>0;\forall x\in TXĐ\)
\(y=-x^4+2x^2+1\Rightarrow y'=-4x^3+4x=0\Rightarrow x=\left\{-1;0;1\right\}\) có cực trị nên có các khoảng ĐB, NB (có thể nhớ nhanh là hàm bậc 4 ko bao giờ ĐB hoặc nghịch biến trên R)
\(y=3x^3+x-3\Rightarrow y'=9x^2+1>0;\forall x\)
Vậy (I) và (III) đồng biến trên các khoảng xác định
A đúng