Kéo một vật m = 200g đi lên một mặt phẳng nghiêng bằng một lực F nằm theo mặt phẳng nghiêng góc nghiêng = 30° hướng lên. Cho biết hệ số ma sát nghỉ =√3/2 , ma sát trượt = √3/4
a) Xác định độ lớn của lực kéo nhỏ nhất để vật trượt từ trạng thái nghỉ.
b) Tính độ lớn lực kéo Fk để vật chuyển động với gia tốc a = 2m/s2
c) Sau 4s kể từ lúc bắt đầu kéo thì ngừng tác dụng lực. Vât sẽ tiếp tục chuyển động như thế nào ? Tính thời gian vật chuyển động trên mặt phẳng nghiêng ?
d) Hỏi khi xuống hết mặt phẳng nghiêng vật còn tiếp tục chuyển động trên mặt phẳng ngang bao lâu và đi được quảng đường dài bao nhiêu ? Cho hệ số ma sát với mặt phẳng ngang = 0,1. Lấy g = 10 m/s2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
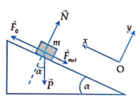
+ Khi vật trượt đều lên mặt phẳng nghiêng:
![]()
Chiếu lên phương mặt phẳng nghiêng và vuông góc với mặt phẳng nghiêng:
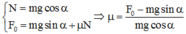
+ Khi vật trượt đều trên mặt ngang:
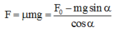

Chọn C.
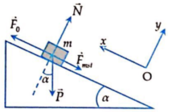
+ Khi vật trượt đều lên mặt phẳng nghiêng:
F 0 ⇀ + P ⇀ + N ⇀ + F m s ⇀ = 0 ⇀
Chiếu lên phương mặt phẳng nghiêng và vuông góc với mặt phẳng nghiêng:
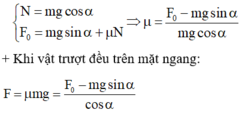

p=mg=20(N)
N=p.cos30
TA có Sin30=4/h ->h=8m
mặt khác Af=FScos0=160
+A/fms=MNScos180= -13,856
+Ap=p.s.cos(90-30)=80

a) Trọng lượng của vật là:
\(P=10.m=10.500=5000\left(N\right)\)
Công để đưa vật lên cao là:
\(A_1=P.h=5000.2=10000\left(J\right)\)
Theo định luật về công, ta có: \(A_1=A_2\)
Chiều dài của mặt phẳng nghiêng là:
\(A_2=F.l\rightarrow l=\dfrac{A_2}{F}=\dfrac{10000}{3500}=\dfrac{20}{7}\left(m\right)\)
b) Hiệu suất của mặt phẳng nghiêng là:
\(H=\dfrac{A_i}{A_{tp}}.100\%=\dfrac{F.l}{F'l}.100\%=\dfrac{F}{F'}.100\%=\dfrac{3500}{4000}.100\%=87,5\%\)