\(A=2x^2-x+20+7\) tìm GTLN của A
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`-2<=x<=2`
`<=>x+2>=0,x-2<=0`
`=>(x+2)(x-2)<=0`
`<=>x^2-4<=0`
`<=>x^2<=4`
`=>A<=4-2x+7=11-2x`
Vì `x>=-2=>2x>=-4`
`=>A<=11+4=15`
Dấu "=" xảy ra khi `x=-2

a: \(B\left(x\right)=-\left(x^2-3x+7\right)\)
\(=-\left(x^2-3x+\dfrac{9}{4}+\dfrac{19}{4}\right)\)
\(=-\left(x-\dfrac{3}{2}\right)^2-\dfrac{19}{4}\le-\dfrac{19}{4}\)
Dấu '=' xảy ra khi x=3/2
b: Ta có: \(C\left(x\right)=-x^2+7x-20\)
\(=-\left(x^2-7x+20\right)\)
\(=-\left(x^2-7x+\dfrac{49}{4}+\dfrac{31}{4}\right)\)
\(=-\left(x-\dfrac{7}{2}\right)^2-\dfrac{31}{4}\le-\dfrac{31}{4}\)
Dấu '=' xảy ra khi x=7/2

Bài 1: (1/2x - 5)20 + (y2 - 1/4)10 < 0 (1)
Ta có: (1/2x - 5)20 \(\ge\)0 \(\forall\)x
(y2 - 1/4)10 \(\ge\)0 \(\forall\)y
=> (1/2x - 5)20 + (y2 - 1/4)10 \(\ge\)0 \(\forall\)x;y
Theo (1) => ko có giá trị x;y t/m
Bài 2. (x - 7)x + 1 - (x - 7)x + 11 = 0
=> (x - 7)x + 1.[1 - (x - 7)10] = 0
=> \(\orbr{\begin{cases}\left(x-7\right)^{x+1}=0\\1-\left(x-7\right)^{10}=0\end{cases}}\)
=> \(\orbr{\begin{cases}x-7=0\\\left(x-7\right)^{10}=1\end{cases}}\)
=> x = 7
hoặc : \(\orbr{\begin{cases}x-7=1\\x-7=-1\end{cases}}\)
=> x = 7
hoặc : \(\orbr{\begin{cases}x=8\\x=6\end{cases}}\)
Bài 3a) Ta có: (2x + 1/3)4 \(\ge\)0 \(\forall\)x
=> (2x +1/3)4 - 1 \(\ge\)-1 \(\forall\)x
=> A \(\ge\)-1 \(\forall\)x
Dấu "=" xảy ra <=> 2x + 1/3 = 0 <=> 2x = -1/3 <=> x = -1/6
Vậy Min A = -1 tại x = -1/6
b) Ta có: -(4/9x - 2/5)6 \(\le\)0 \(\forall\)x
=> -(4/9x - 2/15)6 + 3 \(\le\)3 \(\forall\)x
=> B \(\le\)3 \(\forall\)x
Dấu "=" xảy ra <=> 4/9x - 2/15 = 0 <=> 4/9x = 2/15 <=> x = 3/10
vậy Max B = 3 tại x = 3/10

A=3(x^2+2/3x-1)
=3(x^2+2*x*1/3+1/9-10/9)
=3(x+1/3)^2-10/3>=-10/3
Dấu = xảy ra khi x=-1/3
\(B=1+\dfrac{15}{x^2+x+5}=1+\dfrac{15}{\left(x+\dfrac{1}{2}\right)^2+\dfrac{19}{4}}< =1+15:\dfrac{19}{4}=1+\dfrac{60}{19}=\dfrac{79}{19}\)
Dấu = xảy ra khi x=-1/2


a)A=4(x+11/8)^2 -153/16
Min A=-153/16 khi x=-11/8
b)B=3(x-1/3)^2 -4/3
Min B=-4/3 khi x=1/3
Bài 1:
a) \(A=4x^2+11x-2=\left(4x^2+11x+\dfrac{121}{16}\right)-\dfrac{153}{16}=\left(2x+\dfrac{11}{4}\right)^2-\dfrac{153}{16}\ge-\dfrac{153}{16}\)
\(minA=-\dfrac{153}{16}\Leftrightarrow x=-\dfrac{11}{8}\)
b) \(B=3x^2-2x-1=3\left(x^2-\dfrac{2}{3}x+\dfrac{1}{9}\right)-\dfrac{4}{3}=3\left(x-\dfrac{1}{3}\right)^2-\dfrac{4}{3}\ge-\dfrac{4}{3}\)
\(minB=-\dfrac{4}{3}\Leftrightarrow x=\dfrac{1}{3}\)
Bài 2:
a) \(A=-x^2+3x-1=-\left(x^2-3x+\dfrac{9}{4}\right)+\dfrac{5}{4}=-\left(x-\dfrac{3}{2}\right)^2+\dfrac{5}{4}\le\dfrac{5}{4}\)
\(maxA=\dfrac{5}{4}\Leftrightarrow x=\dfrac{3}{2}\)
b) \(B=-x^2-4x+7=-\left(x^2+4x+4\right)+11=-\left(x+2\right)^2+11\le11\)
\(maxB=11\Leftrightarrow x=-2\)
A = 2x2 - x + 20 + 7
A = 2.(x2 - 2.\(\dfrac{1}{4}\)x + \(\dfrac{1}{16}\) ) + \(\dfrac{215}{8}\)
A = 2.( x - \(\dfrac{1}{4}\))2 + \(\dfrac{215}{8}\)
(x - \(\dfrac{1}{4}\))2 ≥ 0 ⇔ A ≥ \(\dfrac{215}{8}\) ⇔ A(min) = \(\dfrac{215}{8}\) ⇔ x = \(\dfrac{1}{4}\)
ko có A(max) xem lại đề . bạn có thể xem đồ thị trên hình kèm theo ko có A(max)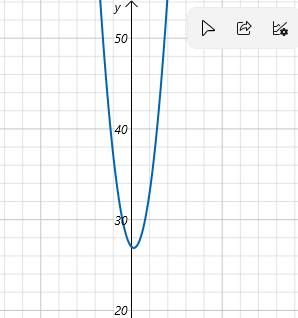
bài toán không có giá trị lớn nhất. xem lại đề nhà bạn