Cho tam giác ABC nhọn. Các đường cao AD, BE, CF cắt nhau tại H. Chứng minh H là tâm đường tròn nội tiếp tam giác DEF.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác BDHF có
góc BDH+góc BFH=180 độ
=>BDHF là tứ giác nội tiếp
b: Xét tứ giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC là tứ giác nội tiếp
c: Xét ΔHAF vuông tại F và ΔHCD vuông tại D có
góc AHF=góc CHD
=>ΔHAF đồng đạng với ΔHCD
=>HA/HC=HF/HD
=>HA*HD=HF*HC
Xét ΔHFB vuông tại F và ΔHEC vuông tại E có
góc FHB=góc EHC
=>ΔHFB đồng dạng vơi ΔHEC
=>HF/HE=HB/HC
=>HF*HC=HB*HE=HA*HD
d: Xét ΔAEF và ΔABC có
góc AEF=góc ABC
góc FAE chung
=>ΔAEF đồng dạng với ΔABC

a) Xét tứ giác BFHD có
\(\widehat{BFH}\) và \(\widehat{BDH}\) là hai góc đối
\(\widehat{BFH}+\widehat{BDH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BFHD là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
\(\widehat{BFC}\) và \(\widehat{BEC}\) cùng nhìn cạnh BC một góc bằng 900
Do đó: BFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

xét tứ giác BFHD có
góc BFH + góc BDH = 180
mà nó là 2 góc đối => nội tiếp => góc FDH = góc FBE
chứng minh tương tự với tứ giác CEHD
=> góc HDE = góc HCE
Xét tứ giác BFEC có
góc BFC = góc BEF = 90
mà nó là 2 góc kề => tứ giác nội tiếp
mà góc BEC = 1/2 sđ BC = 90 => SĐ BC = 180 => BC là đường kính mà I là trung điểm BC => I là tâm đường tròn ngoại tiếp tứ giác BFEC
=> góc FIE = góc FBE + góc FCE
=> Góc FIE = góc FDH+góc HDE => góc FIE = góc FDE
mà nó là 2 góc kề => nội tiếp
=> điều phải cm

a, E, F cùng nhìn BC dưới 1 góc 90 => tứ giác BFEC nội tiếp
cmtt F,E cung nhìn AH dưới 1 góc 90 => tứ giác AEHF nội tiếp =>góc EHC = góc BAC ( cùng bù với EHF)
b, Xét tam giác ABE và tam giác CHE có
góc BAC = góc EHC
góc BEA = góc CEH = 90
=>tam giác BAE đồng dạng với tam giác CHE(gg) =>AE/HE=BE/CE=> EA.EC=EH.EC
c,cmtt câu a, ta được tứ giác BFHD =>góc ABE = góc FDA
tứ giác DHEC nội tiếp =>góc ADE = góc FCA
Lại có góc ABE = góc FCA vì cùng phụ với góc BAC => góc FDA=góc ADE => AD là phân giác của góc FDE
cmtt =>FC và EB là phân giác của góc DFE và DEF
=> H là tâm đường tròn nội tiếp tam giác DEF

a: Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=180^0\)
nên AEHF là tứ giác nội tiếp
b: Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp
=>\(\widehat{FEC}+\widehat{ABC}=180^0\)

a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{FAC}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC
Suy ra: \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
hay \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
\(\widehat{FAC}\) chung
Do đó: ΔAEF\(\sim\)ΔABC

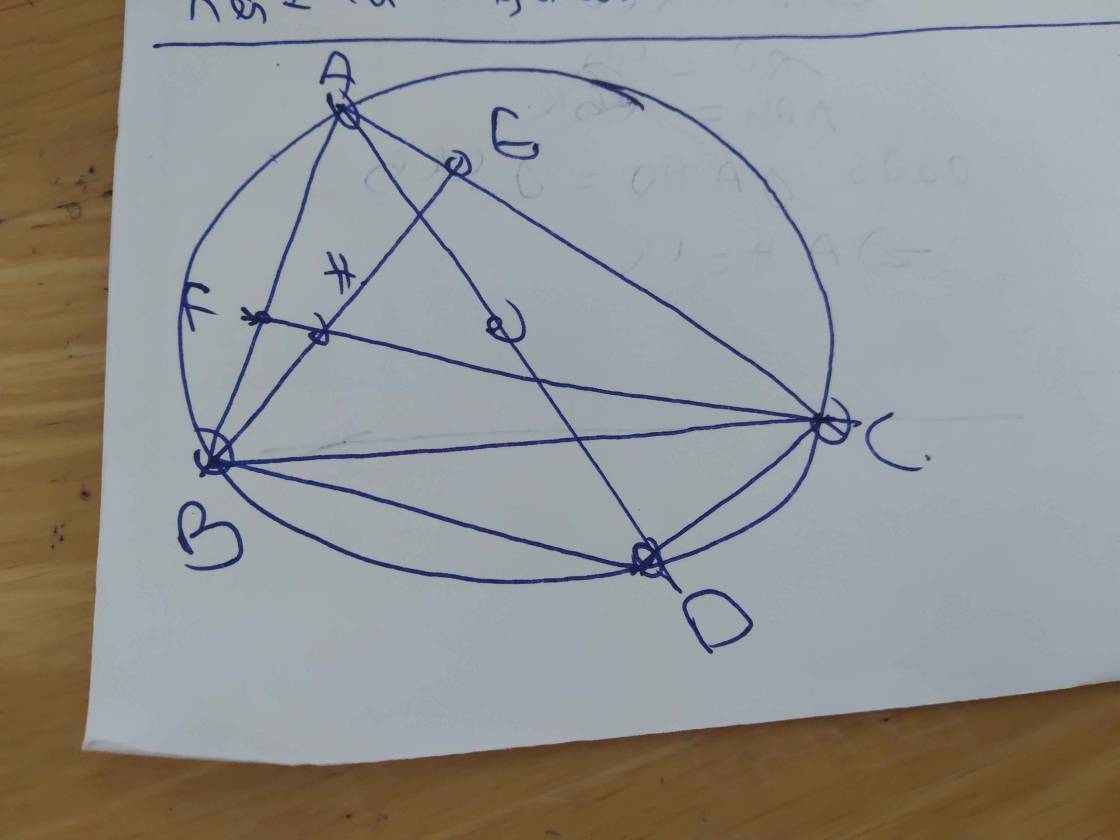


Đề thì đúng nhưng đề này là đề học sinh giỏi thì thường quá!
Bạn chỉ cần dùng tứ giác nội tiếp là sẽ ra \(DH\) là phân giác \(\widehat{EDF}\) (tin mình đi). Tương tự với mấy đỉnh kia suy ra đpcm.
sai đề rồi đáng lẽ ABC là tam giác đều hoặc các đường cao AD BE CF là những đường trung trực