Cho ham so y = f(x) = I3-4xI. Tim x0 de f(x0) =f(-x0).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt 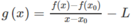
Suy ra g(x) xác định trên
(
a
;
b
)
\
x
0
và 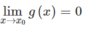
Mặt khác, f ( x ) = f ( x 0 ) + L ( x − x 0 ) + ( x − x 0 ) g ( x ) nên
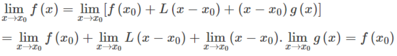
Vậy hàm số y = f(x) liên tục tại

Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng

Đáp án là A
Theo điều đủ để hàm số có cực trị thì x 0 là điểm cực tiểu của hàm số.


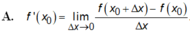
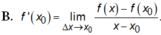
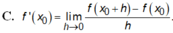
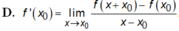
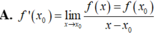
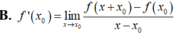
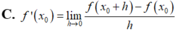


Ta có :
\(\left|3-4x_0\right|=\left|3-4.\left(-x_0\right)\right|\)
\(\Leftrightarrow\left|3-4x_0\right|=\left|3+4x_0\right|\)
TH1 : \(x_0< -\frac{3}{4}:\)
\(\Leftrightarrow3-4x_0=-\left(3+4x_0\right)\)
\(\Leftrightarrow3+3=8x_0\)
\(\Leftrightarrow x_0=\frac{3}{4}\) ( Không thỏa mãn )
TH2 : \(-\frac{3}{4}\le x_0\le\frac{3}{4}\)
Giải tương tự thì có \(x_0=0\)
TH3 : \(x_0>\frac{3}{4}\)
Giải tương tự thì ko có giá trị thỏa mãn.
Vậy ...