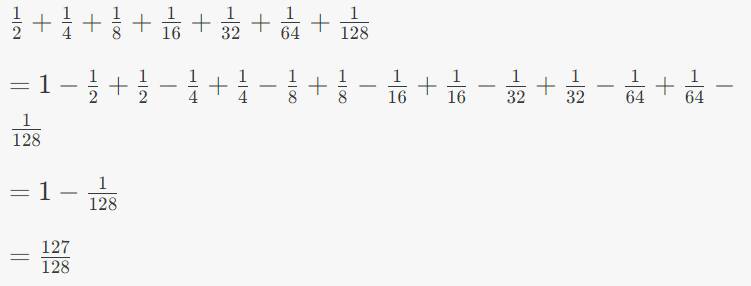\(E=\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+...+\dfrac{1}{256}\)

\(2\times E=1+\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{128}\)

\(2\times E-E=\left(1+\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{128}\right)-\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{256}\right)\)

\(E=1-\dfrac{1}{256}\)

\(E=\dfrac{256}{256}-\dfrac{1}{256}\)

\(E=\dfrac{255}{256}\)

=255/256

~hok tốt~

#Trang#

Tính \(S=\frac{1}{2}+\frac{1}{4}+...+\frac{1}{256}\)

Dùng sai phân như sau

\(2S-S=\left(1+\frac{1}{2}+\frac{1}{4}+...+\frac{1}{128}\right)-\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{256}\right)=1-\frac{1}{256}\)

Vậy \(S=1-\frac{1}{256}\)

\(\text{Đặt }\)\(A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}+\frac{1}{256}\)

\(\Rightarrow2A=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)

\(\Rightarrow2A-A=1-\frac{1}{256}\)

\(=>A=\frac{255}{256}\)

1/2+1/4+1/8+1/16+1/32+1/64+1/128+1/256=247/256

1 / 2 + 1 / 4 + 1 / 8 + 1 / 16 + 1 / 32 + 1 / 64 + 1 / 128 = 127 / 128

ý bạn là + 1/256 chứ j

KQ bằng 255/256.

A= 1/2 + 1/4+ 1/8+ 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + 1/512 
A = 1 - 1/2 + 1/2- 1/4 + 1/4 - 1/8 + 1/8 - 1/16 + 1/16 - 1/32 + 1/32 - 1/64 + 1/64 - 1/128 + 1/128 - 1/256 - 1/256 - 1/512 
A = 1 - 1/512 
A = 511/512 
Chúc bạn học giỏi nha!

gọi biểu thức đó là A

A=1/2+1/4+1/8+1/16+1/32+1/64+1/128+1/256+1/512

1/512+A=1/2+1/4+1/8+1/16+1/32+1/64+1/128+1/256+1/512+1/512

1/512+A=1/2+1/4+1/8+1/16+1/32+1/64+1/128+1/256+1/256

1/512+A=1/2+1/4+1/8+1/16+1/32+1/64+1/128+1/128

1/512+A=1/2+1/4+1/8+1/16+1/32+1/64+1/64

1/512+A=1/2+1/4+1/8+1/16+1/32+1/32

1/512+A=1/2+1/4+1/8+1/16+1/16

1/512+A=1/2+1/4+1/8+1/8

1/512+A=1/2+1/4+1/4

1/512+A=1/2+1/2

1/512+A=1

A=1-1/512

A=511/512

chắc 100%

*Tham khảo 

b-1/2+1/4+1/8+1/16+1/32+1/64+1/128+1/256