Cho tam giác ABC nhọn, các đường cao AD và BE cắt nhau tại H. Qua A kẻ đường thẳng song song với BC, qua B kẻ đường thẳng song song với AD, chúng cắt nhau tại M. Chứng minh: Nếu: \(AC^2=4BE.HE\) thì tam giác ABC là tam giác cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b: góc DFC=góc EBC
góc EFC=góc DAC
góc EBC=góc DAC
=>góc DFC=góc EFC

Gọi diện tích các hình tam giác ABC, MAB, MAC, MBC lần lượt là S, S 1 , S 2 , S 3 . Ta có:
S = S 1 + S 2 + S 3
Trong đó: S = 1/2 AD.BC = 1/2 BE. AC = 1/2 CF. AB
S 1 = 1/2 MT. AB
S 2 = 1/2 MK. AC
S 3 = 1/2 MH. BC
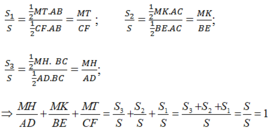

a/
Ta có D và E cùng nhìn HC dưới 1 góc vuông nên D và E thuộc đường tròn đường kính HC => CDHE là tứ giác nội tiếp
Ta có E và F cùng nhìn BC dưới 1 góc vuông nên E và F thuộc đường tròn đường kính BC => BCEF là tứ giác nội tiếp
b/ Xét tg MEB và tg MCF có
\(\widehat{EMC}\) chung
\(\widehat{MEB}=\widehat{MCF}\) (góc nội tiếp cùng chắn cung BF)
=> tg MEB đồng dạng với tg MCF (g.g.g)
\(\Rightarrow\dfrac{ME}{MC}=\dfrac{MB}{MF}\Rightarrow MB.MC=ME.MF\)

a) Xét ΔABC có
BE là đường cao ứng với cạnh AC(gt)
CF là đường cao ứng với cạnh AB(gt)
BE cắt CF tại H(gt)
Do đó: H là trực tâm của ΔABC(Tính chất ba đường cao của tam giác)
Suy ra: AH⊥BC
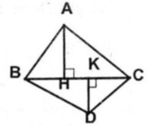
b) Xét tứ giác BHCK có
HC//BK(gt)
BH//CK(gt)
Do đó: BHCK là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Suy ra: Hai đường chéo HK và BC cắt nhau tại trung điểm của mỗi đường(Định lí hình bình hành)
mà M là trung điểm của BC(gt)
nên M là trung điểm của HK
hay H,M,K thẳng hàng(đpcm)
Ta có: AEH=90⁰.
=>HAE+AHE=90⁰.(1)
Ta có: ∆BHD vuông tại D.
=>DBH+BHD=90⁰.(2)
Từ (1) và (2) suy ra: HAE+AHE=DBH+BHD=90⁰.
Mà: AHE=DBH (2 góc đối đỉnh).
=> HAE=DBH.
=>HAE=DBE.
=>∆HEA~CBE(g.g).
=>AE/BE=HE/CE.
=>BE.HE=AE.CE.=>4BE.HE=4AE.CE.=>4BE.HE=AC².
=> (AE+CE)²=4AE.CE.
=>(AE-CE)²=0.
=>AE=CE
=> E là trung điểm của AC
=> BE là đường trung tuyến của ∆ABC
Mà: BE là đường cao của ∆ABC.
=> ∆ABC cân tại B.