giải giúp mình nhanh với ạ.Mình đang rất cần
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Đầu tiên bạn cần xác định được alen trội và lặn. Ví dụ như ta quy ước $A$ là quả to là trội, còn $a$ là quả bé lặn.
- Tiếp theo là ở $P$ thì nếu bài nói quả to thuần chủng thì tức kiểu gen ở đây là $AA$ còn nếu không thuần chủng thì là $Aa$ còn nếu nói quả to không thì có 2 trường hợp.
- Ví dụ như ở phép lai giữa quả to thuần chủng với quả nhỏ.
$P:$ $AA$ \(\times\) \(aa\)
$Gp:$ $A$ $a$
$F_1:$ $Aa$
- Ở $Gp$ thì bạn cần phải rõ là $AA$ sẽ tạo ra $A$ còn $Aa$ sẽ tạo ra 2 giao tử $A,a$ và kết hợp với giao tử bên còn lại tạo $F1$
- Ở phép lai 1 cặp tính trạng có 6 trường hợp:
\(1.\) \(P:AA\times AA\rightarrow F_1:100\%AA\)
\(2.\) \(P:AA\times Aa\rightarrow F_1:50\%AA;50\%Aa\)
\(3.\) \(P:AA\times aa\rightarrow F_1:100\%Aa\)
\(4.\) \(P:Aa\times Aa\rightarrow F_1:25\%AA;50\%Aa;25\%aa\)
\(5.\) \(P:Aa\times aa\rightarrow F_1:50\%Aa;50\%aa\)
\(6.\) \(P:aa\times aa\rightarrow F_1:100\%aa\)



Tham khảo
Không thể có tình bạn một phía để xây dựng một tình bạn trong sáng, lành mạnh phải có thiện chí và cố gắng từ cả hai phía.

a) xét delta phẩy ta có b'2 - ac
<=> 4 - m
b) để pt 1 luôn có nghiệm thì delta phẩy ≥ 0
=> 4-m ≥ 0 => m ≤ 4
c) xét delta phẩy của pt (1) ta có
4 - m để pt có 2 nghiệm x1,x2 thì delta phẩy ≥ 0 => m ≤ 4
theo Vi-ét ta có:\(\left\{{}\begin{matrix}x1+x2=4\\x1x2=m\end{matrix}\right.\)
theo bài ra ta có: x12 + x22 = 12 <=> ( x1+x2 )2 - 2x1x2 = 12
<=> 16 - 2m -12 = 0 <=> 2m = 4 <=> m = 2 ( thỏa đk)
vậy m = 2 thì pt thỏa mãn điều kiện.
d) A= x12 + x22
<=> A = (x1+x2)2 - 2x1x2
<=> A = 16 - 2m ta có m ≤ 4
nên giá trị lớn nhất của m = 4
vậy giá trị nhỏ nhất của A = 16 - 2.4
GTNN của A = 8 dấu "=" xảy ra khi m = 4
a) Ta có: a = 1 ; b' = -2 ; c = m
⇒ △' = b'2 - ac = ( -2 )2 - 1 .m = 4 - m
b) Để phương trình luôn có nghiệm thì △' \(\ge\) 0
⇒ 4 - m \(\ge\) 0 ⇔ m \(\le\) 4
Vậy khi m \(\le\) 4 thì phương trình luôn có nghiệm
c) Theo câu (b) thì phương trình luôn có nghiệm khi m \(\le\) 4
Theo hệ thức Vi - ét ta có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=4\\x_1x_2=\dfrac{c}{a}=m\end{matrix}\right.\)
Do đó:
\(x_1^2+x_2^2=12\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=12\)
\(\Leftrightarrow4^2-2m=12\)
\(\Leftrightarrow4=2m\Leftrightarrow m=2\)
Vậy khi m = 2 thì phương trình (1) có 2 nghiệm x1 ; x2 thỏa mãn x12 + x22 = 12

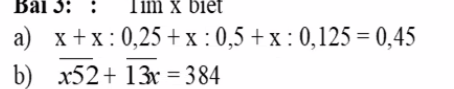

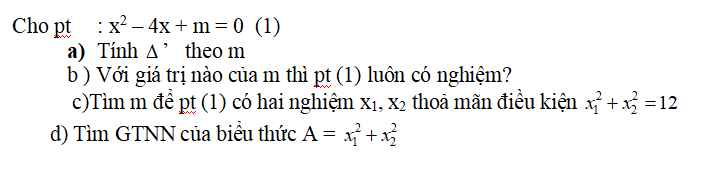 giúp mình với ạ.Mình cần lời giải chi tiết
giúp mình với ạ.Mình cần lời giải chi tiết
đề bài đâu bạn
đề bài ở dưới nha