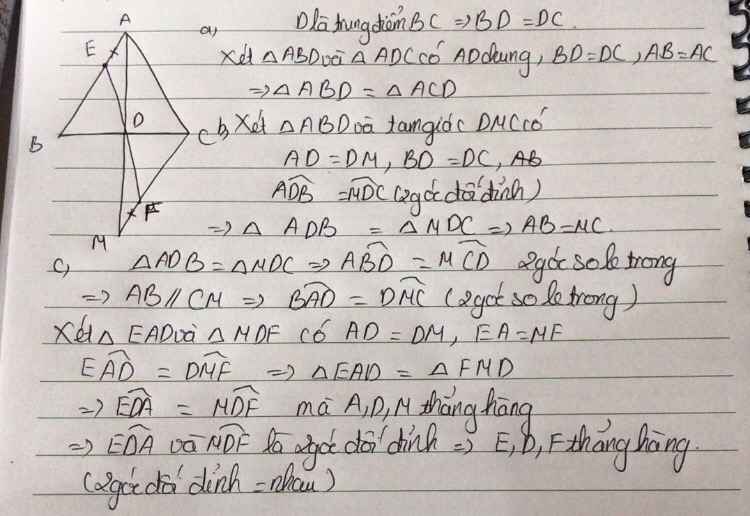Cho ABC vuông tại A có B = C. Kẻ AH vuông góc với BC(H BC). Chứng minh rằng AH là tia phân giác của góc A.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
Do đó: ΔOAM=ΔOBM
Suy ra: MA=MB
b: Xét ΔOAH vuông tại A và ΔOBK vuông tại B có
OA=OB
\(\widehat{AOH}\) chung
Do đó: ΔOAH=ΔOBK
Suy ra: OH=OK
hay ΔOHK cân tại O
d: Ta có: ΔOHK cân tại O
mà OM là đường phân giác
nên OM là đường trung tuyến ứng với cạnh HK
mà G là trung điểm của HK
nên O,M,G thẳng hàng

b1
a) CM tam giác chứaHB và chứa HC = nhau
b) CM tam giác chứa 2 góc A = nhau

a: Xét ΔAHB vuông tại H và ΔAHK vuông tại H có
AH chung
HB=HK
Do đó: ΔAHB=ΔAHK

a: Xét ΔBAD và ΔCAD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔABD=ΔACD

a) Xét ΔEHB vuông tại E và ΔDHC vuông tại D có
\(\widehat{EHB}=\widehat{DHC}\)(hai góc đối đỉnh)
Do đó: ΔEHB∼ΔDHC(g-g)
Suy ra: \(\dfrac{HE}{HD}=\dfrac{HB}{HC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{HE}{HB}=\dfrac{HD}{HC}\)
Xét ΔHED và ΔHBC có
\(\dfrac{HE}{HB}=\dfrac{HD}{HC}\)(cmt)
\(\widehat{EHD}=\widehat{BHC}\)(hai góc đối đỉnh)
Do đó: ΔHED∼ΔHBC(c-g-c)
b) Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{EAC}\) chung
Do đó: ΔADB∼ΔAEC(g-g)
Suy ra: \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét ΔADE và ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)(cmt)
\(\widehat{EAD}\) chung
Do đó: ΔADE∼ΔABC(c-g-c)